Question Number 7482 by kishanjith last updated on 31/Aug/16

$$\int\frac{\left(\mathrm{1}+{x}\right)^{−\mathrm{2}/\mathrm{3}} }{\left(\mathrm{1}+{x}\right)}{dx} \\ $$
Answered by sandy_suhendra last updated on 31/Aug/16
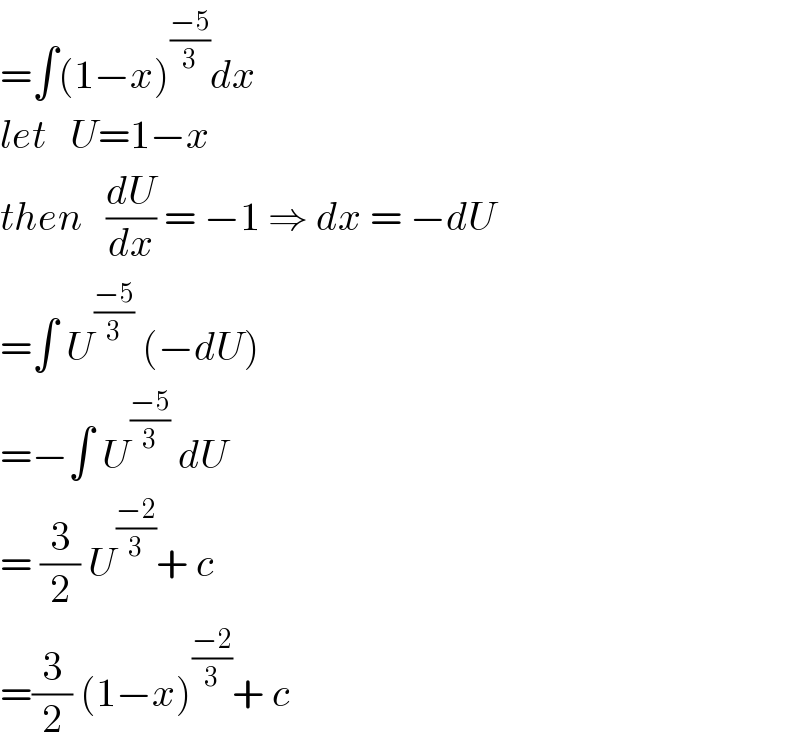
$$=\int\left(\mathrm{1}−{x}\right)^{\frac{−\mathrm{5}}{\mathrm{3}}} {dx} \\ $$$${let}\:\:\:{U}=\mathrm{1}−{x}\: \\ $$$${then}\:\:\:\frac{{dU}}{{dx}}\:=\:−\mathrm{1}\:\Rightarrow\:{dx}\:=\:−{dU} \\ $$$$=\int\:{U}^{\frac{−\mathrm{5}}{\mathrm{3}}} \:\left(−{dU}\right) \\ $$$$=−\int\:{U}^{\frac{−\mathrm{5}}{\mathrm{3}}} \:{dU} \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{2}}\:{U}^{\frac{−\mathrm{2}}{\mathrm{3}}} +\:{c} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\:\left(\mathrm{1}−{x}\right)^{\frac{−\mathrm{2}}{\mathrm{3}}} +\:{c} \\ $$
