Question Number 76468 by kaivan.ahmadi last updated on 27/Dec/19
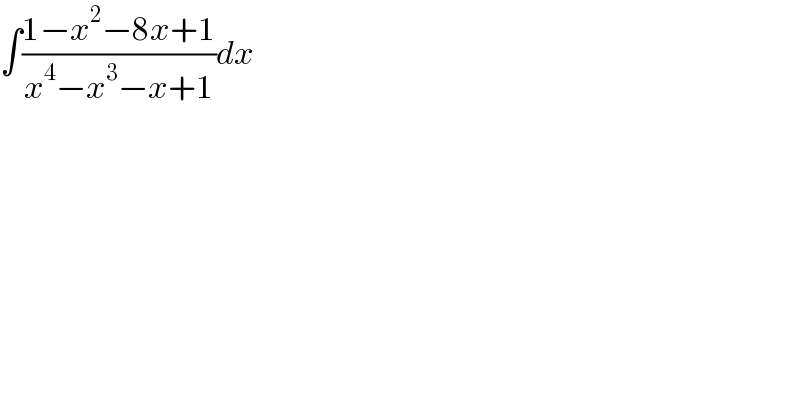
$$\int\frac{\mathrm{1}−{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{1}}{{x}^{\mathrm{4}} −{x}^{\mathrm{3}} −{x}+\mathrm{1}}{dx} \\ $$
Commented by mr W last updated on 27/Dec/19
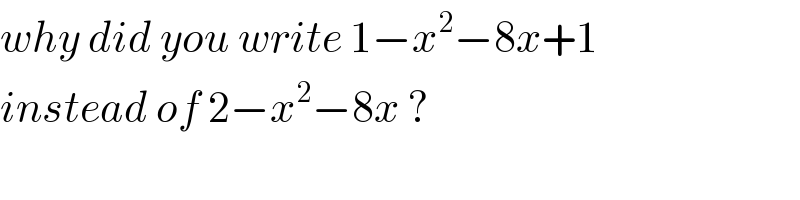
$${why}\:{did}\:{you}\:{write}\:\mathrm{1}−{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{1} \\ $$$${instead}\:{of}\:\mathrm{2}−{x}^{\mathrm{2}} −\mathrm{8}{x}\:? \\ $$
Commented by kaivan.ahmadi last updated on 27/Dec/19

$${i}\:{dont}\:{know}.{it}\:{is}\:{a}\:{practice}\:{that}\:{i}\:{saw}\:{it}. \\ $$
Answered by MJS last updated on 27/Dec/19
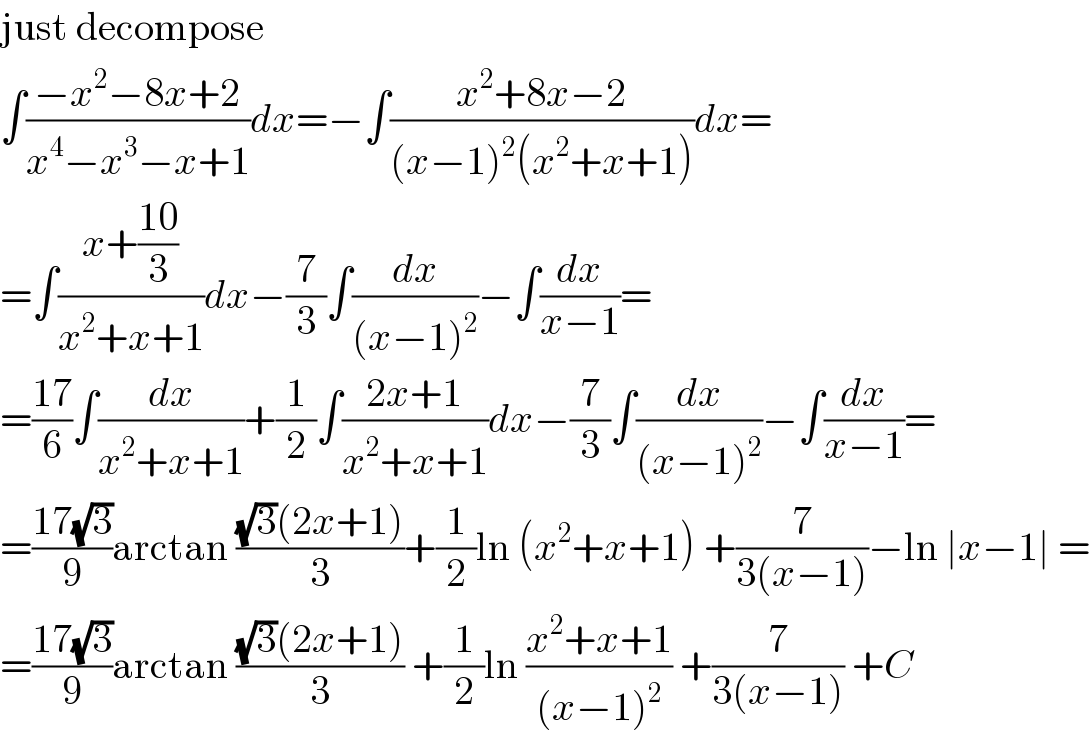
$$\mathrm{just}\:\mathrm{decompose} \\ $$$$\int\frac{−{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{2}}{{x}^{\mathrm{4}} −{x}^{\mathrm{3}} −{x}+\mathrm{1}}{dx}=−\int\frac{{x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{2}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}{dx}= \\ $$$$=\int\frac{{x}+\frac{\mathrm{10}}{\mathrm{3}}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}−\frac{\mathrm{7}}{\mathrm{3}}\int\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }−\int\frac{{dx}}{{x}−\mathrm{1}}= \\ $$$$=\frac{\mathrm{17}}{\mathrm{6}}\int\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}−\frac{\mathrm{7}}{\mathrm{3}}\int\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }−\int\frac{{dx}}{{x}−\mathrm{1}}= \\ $$$$=\frac{\mathrm{17}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\:+\frac{\mathrm{7}}{\mathrm{3}\left({x}−\mathrm{1}\right)}−\mathrm{ln}\:\mid{x}−\mathrm{1}\mid\:= \\ $$$$=\frac{\mathrm{17}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{7}}{\mathrm{3}\left({x}−\mathrm{1}\right)}\:+{C} \\ $$
Commented by kaivan.ahmadi last updated on 29/Dec/19

$${thank}\:{you}\:{sir} \\ $$
