1-x-2-x-2-dx-

Question Number 66096 by sitangshu17 last updated on 09/Aug/19

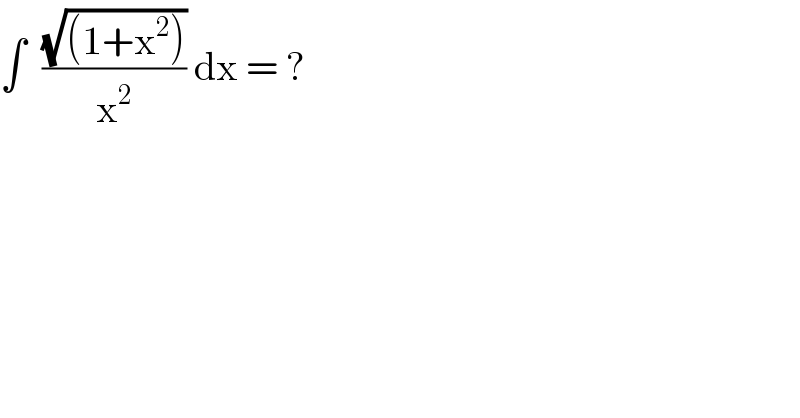
$$\int\:\:\frac{\sqrt{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}}{\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=\:? \\ $$

Commented by mathmax by abdo last updated on 09/Aug/19

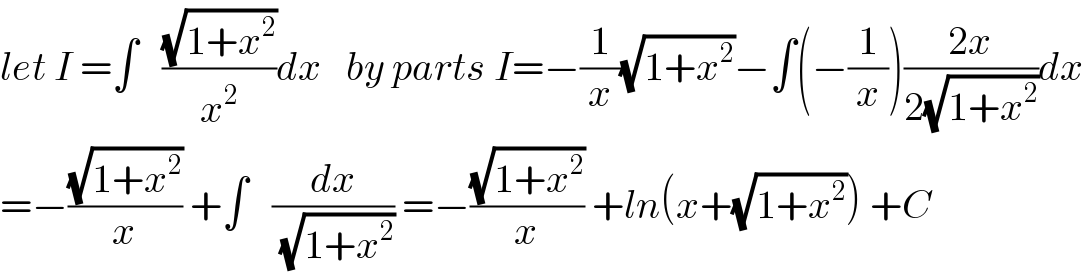
let I =∫ ((√(1+x^2 ))/x^2 )dx by parts I=−(1/x)(√(1+x^2 ))−∫(−(1/x))((2x)/(2(√(1+x^2 ))))dx =−((√(1+x^2 ))/x) +∫ (dx/( (√(1+x^2 )))) =−((√(1+x^2 ))/x) +ln(x+(√(1+x^2 ))) +C

$${let}\:{I}\:=\int\:\:\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }{dx}\:\:\:{by}\:{parts}\:{I}=−\frac{\mathrm{1}}{{x}}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\int\left(−\frac{\mathrm{1}}{{x}}\right)\frac{\mathrm{2}{x}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{dx} \\ $$$$=−\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\:+\int\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:=−\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\:+{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:+{C} \\ $$

Commented by Prithwish sen last updated on 09/Aug/19

put 1+x^2 =x^2 z^2 (dx/x) = ((zdz)/(1−z^2 )) ∫((√(1+x^2 ))/x^2 ) dx = ∫((xz)/x^2 )dx =∫((zdx)/x) = ∫(z^2 /(1−z^2 ))dz =∫[(1/(1−z^2 )) −1]dz = (1/2)ln∣((x+(√(1+x^2 )))/(x−(√(1+x^2 ))))∣−((√(1+x^2 ))/x) +C by putting z=((√(1+x^2 ))/x) please check

$$\mathrm{put}\:\mathrm{1}+\mathrm{x}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} \mathrm{z}^{\mathrm{2}} \\ $$$$\frac{\mathrm{dx}}{\mathrm{x}}\:=\:\frac{\mathrm{zdz}}{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }\:\:\: \\ $$$$\int\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=\:\int\frac{\mathrm{xz}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\int\frac{\mathrm{zdx}}{\mathrm{x}}\:=\:\int\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }\mathrm{dz} \\ $$$$=\int\left[\frac{\mathrm{1}}{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }\:−\mathrm{1}\right]\mathrm{dz}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}−\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mid−\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}}\:+\mathrm{C} \\ $$$$\mathrm{by}\:\mathrm{putting}\:\mathrm{z}=\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}}\:\:\mathrm{please}\:\mathrm{check} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply