Menu Close

1-x-5-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 75446 by Crabby89p13 last updated on 11/Dec/19
∫(1/(x^5 −1))dx
$$\int\frac{\mathrm{1}}{{x}^{\mathrm{5}} −\mathrm{1}}{dx} \\ $$
Answered by MJS last updated on 11/Dec/19
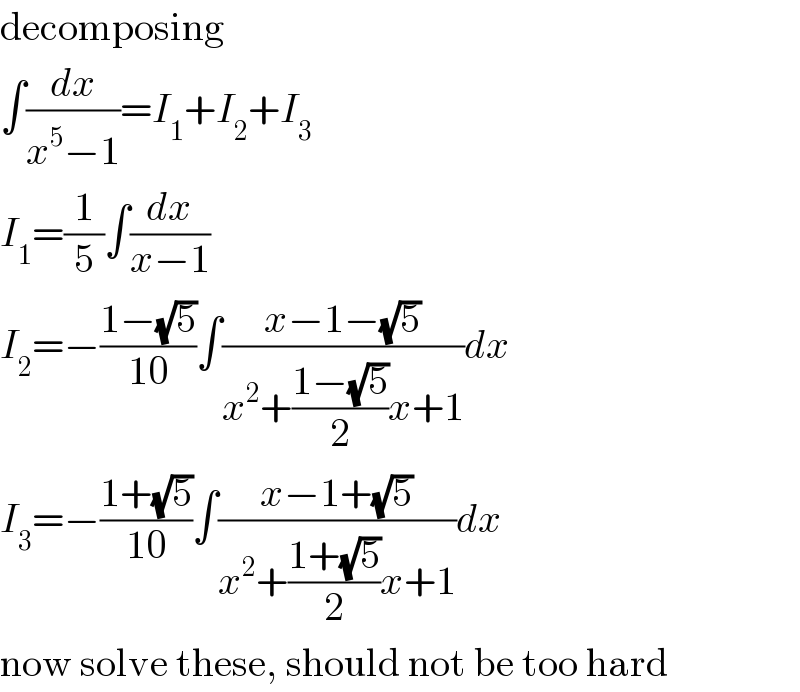
decomposing ∫(dx/(x^5 −1))=I_1 +I_2 +I_3 I_1 =(1/5)∫(dx/(x−1)) I_2 =−((1−(√5))/(10))∫((x−1−(√5))/(x^2 +((1−(√5))/2)x+1))dx I_3 =−((1+(√5))/(10))∫((x−1+(√5))/(x^2 +((1+(√5))/2)x+1))dx now solve these, should not be too hard
$$\mathrm{decomposing} \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{5}} −\mathrm{1}}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} +{I}_{\mathrm{3}} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{dx}}{{x}−\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{10}}\int\frac{{x}−\mathrm{1}−\sqrt{\mathrm{5}}}{{x}^{\mathrm{2}} +\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}}{dx} \\ $$$${I}_{\mathrm{3}} =−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{10}}\int\frac{{x}−\mathrm{1}+\sqrt{\mathrm{5}}}{{x}^{\mathrm{2}} +\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}}{dx} \\ $$$$\mathrm{now}\:\mathrm{solve}\:\mathrm{these},\:\mathrm{should}\:\mathrm{not}\:\mathrm{be}\:\mathrm{too}\:\mathrm{hard} \\ $$
Commented by Crabby89p13 last updated on 12/Dec/19
thanks
$${thanks} \\ $$
Commented by vishalbhardwaj last updated on 12/Dec/19
sir how did you decompose this , please write complete explanation
$$\mathrm{sir}\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{decompose}\:\mathrm{this} \\ $$$$,\:\mathrm{please}\:\mathrm{write}\:\mathrm{complete}\:\mathrm{explanation} \\ $$
Commented by MJS last updated on 12/Dec/19
the roots of x^5 −1=0 x^5 −1=0 x_1 =1 (x−1)(x^4 +x^3 +x^2 +x+1)=0 x^4 +x^3 +x^2 +x+1=0 x=t−(1/4) t^4 +(5/8)t^2 +(5/8)t+((205)/(256))=0 finding the 2 square factors to get (t^2 −αt−β)(t^2 +αt−γ)=0 t^4 −(α^2 +β+γ)t^2 −α(β−γ)t+βγ=0 comparing constant factors (1) −(α^2 +β+γ)=(5/8) (2) −α(β−γ)=(5/8) (3) βγ=((205)/(256)) (1) ⇒ γ=−α^2 −β−(5/8) (2) ⇒ β=γ−(5/(8α)) ⇒_((1)) β=−(α^2 /2)−(5/(16α))−(5/(16)) (3) ⇒_((1)&(2)) (α^4 /4)+((5α^2 )/(16))−((25)/(256α^2 ))−((45)/(64))=0 α^6 +(5/4)α^4 −((45)/(16))α^2 −((25)/(64))=0 α=(√p) p^3 +(5/4)p^2 −((45)/(16))p−((25)/(64))=0 p=q−(5/(12)) q^3 −((10)/3)q+((25)/(27))=0 trying factors of ((25)/(27)) ⇒ q_1 =(5/3) ⇒ p=(5/4) ⇒ α=((√5)/2) ⇒ β=−((15)/(16))−((√5)/8) ⇒ γ=−((15)/(16))+((√5)/8) ⇒ t^4 +(5/8)t^2 +(5/8)t+((205)/(256))=(t^2 −((√5)/2)t+((15+2(√5))/(16)))(t^2 +((√5)/2)t+((15−2(√5))/(16))) t=x+(1/4) ⇒ x^5 −1=(x−1)(x^2 +((1−(√5))/2)x+1)(x^2 +((1+(√5))/2)x+1) decomposing (a/(x−1))+((bx+c)/(x^2 +((1−(√5))/2)x+1))+((dx+e)/(x^2 +((1+(√5))/2)x+1))=(1/(x^5 −1)) ...transforming leads to the system a+b+d=0 a−((1−(√5))/2)b+c−((1+(√5))/2)d+e=0 a+((1−(√5))/2)b−((1−(√5))/2)c+((1+(√5))/2)d−((1+(√5))/2)e=0 a−b+((1−(√5))/2)c−d+((1+(√5))/2)e=0 a−c−e−1=0 ⇒ a=(1/5) b=−((1−(√5))/(10)) c=−(2/5) d=−((1+(√5))/(10)) e=−(2/5)
$$\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:{x}^{\mathrm{5}} −\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{5}} −\mathrm{1}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{1} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}={t}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${t}^{\mathrm{4}} +\frac{\mathrm{5}}{\mathrm{8}}{t}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{8}}{t}+\frac{\mathrm{205}}{\mathrm{256}}=\mathrm{0} \\ $$$$\mathrm{finding}\:\mathrm{the}\:\mathrm{2}\:\mathrm{square}\:\mathrm{factors}\:\mathrm{to}\:\mathrm{get} \\ $$$$\left({t}^{\mathrm{2}} −\alpha{t}−\beta\right)\left({t}^{\mathrm{2}} +\alpha{t}−\gamma\right)=\mathrm{0} \\ $$$${t}^{\mathrm{4}} −\left(\alpha^{\mathrm{2}} +\beta+\gamma\right){t}^{\mathrm{2}} −\alpha\left(\beta−\gamma\right){t}+\beta\gamma=\mathrm{0} \\ $$$$\mathrm{comparing}\:\mathrm{constant}\:\mathrm{factors} \\ $$$$\left(\mathrm{1}\right)\:\:−\left(\alpha^{\mathrm{2}} +\beta+\gamma\right)=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\left(\mathrm{2}\right)\:\:−\alpha\left(\beta−\gamma\right)=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\left(\mathrm{3}\right)\:\:\beta\gamma=\frac{\mathrm{205}}{\mathrm{256}} \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:\gamma=−\alpha^{\mathrm{2}} −\beta−\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\left(\mathrm{2}\right)\:\Rightarrow\:\beta=\gamma−\frac{\mathrm{5}}{\mathrm{8}\alpha}\:\:\underset{\left(\mathrm{1}\right)} {\Rightarrow}\:\:\beta=−\frac{\alpha^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{16}\alpha}−\frac{\mathrm{5}}{\mathrm{16}} \\ $$$$\left(\mathrm{3}\right)\:\:\underset{\left(\mathrm{1}\right)\&\left(\mathrm{2}\right)} {\Rightarrow}\:\:\:\:\frac{\alpha^{\mathrm{4}} }{\mathrm{4}}+\frac{\mathrm{5}\alpha^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{25}}{\mathrm{256}\alpha^{\mathrm{2}} }−\frac{\mathrm{45}}{\mathrm{64}}=\mathrm{0} \\ $$$$\:\:\:\:\:\alpha^{\mathrm{6}} +\frac{\mathrm{5}}{\mathrm{4}}\alpha^{\mathrm{4}} −\frac{\mathrm{45}}{\mathrm{16}}\alpha^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{64}}=\mathrm{0} \\ $$$$\:\:\:\:\:\alpha=\sqrt{{p}} \\ $$$$\:\:\:\:\:{p}^{\mathrm{3}} +\frac{\mathrm{5}}{\mathrm{4}}{p}^{\mathrm{2}} −\frac{\mathrm{45}}{\mathrm{16}}{p}−\frac{\mathrm{25}}{\mathrm{64}}=\mathrm{0} \\ $$$$\:\:\:\:\:{p}={q}−\frac{\mathrm{5}}{\mathrm{12}} \\ $$$$\:\:\:\:\:{q}^{\mathrm{3}} −\frac{\mathrm{10}}{\mathrm{3}}{q}+\frac{\mathrm{25}}{\mathrm{27}}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{trying}\:\mathrm{factors}\:\mathrm{of}\:\frac{\mathrm{25}}{\mathrm{27}}\:\Rightarrow\:{q}_{\mathrm{1}} =\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\Rightarrow\:{p}=\frac{\mathrm{5}}{\mathrm{4}}\:\Rightarrow\:\alpha=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:\Rightarrow\:\beta=−\frac{\mathrm{15}}{\mathrm{16}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{8}}\:\Rightarrow\:\gamma=−\frac{\mathrm{15}}{\mathrm{16}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$\Rightarrow \\ $$$${t}^{\mathrm{4}} +\frac{\mathrm{5}}{\mathrm{8}}{t}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{8}}{t}+\frac{\mathrm{205}}{\mathrm{256}}=\left({t}^{\mathrm{2}} −\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}{t}+\frac{\mathrm{15}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right)\left({t}^{\mathrm{2}} +\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}{t}+\frac{\mathrm{15}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right) \\ $$$${t}={x}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{5}} −\mathrm{1}=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{decomposing} \\ $$$$\frac{{a}}{{x}−\mathrm{1}}+\frac{{bx}+{c}}{{x}^{\mathrm{2}} +\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}}+\frac{{dx}+{e}}{{x}^{\mathrm{2}} +\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}}=\frac{\mathrm{1}}{{x}^{\mathrm{5}} −\mathrm{1}} \\ $$$$…\mathrm{transforming}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{the}\:\mathrm{system} \\ $$$${a}+{b}+{d}=\mathrm{0} \\ $$$${a}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{b}+{c}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{d}+{e}=\mathrm{0} \\ $$$${a}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{b}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{c}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{d}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{e}=\mathrm{0} \\ $$$${a}−{b}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{c}−{d}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{e}=\mathrm{0} \\ $$$${a}−{c}−{e}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\: \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${b}=−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$$${c}=−\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${d}=−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$$${e}=−\frac{\mathrm{2}}{\mathrm{5}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *