Question Number 12797 by tawa last updated on 01/May/17
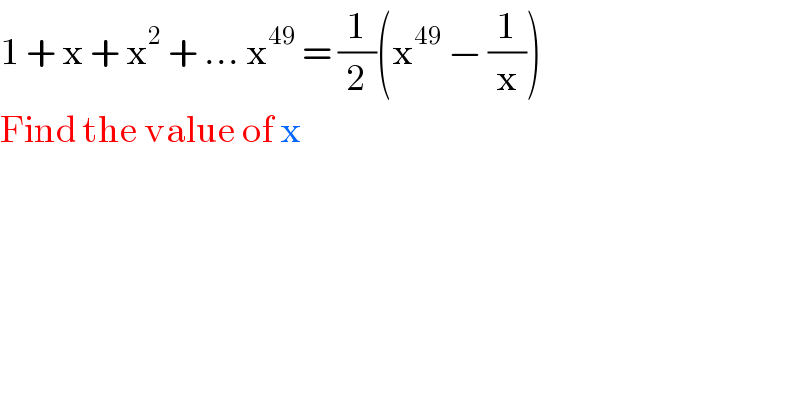
$$\mathrm{1}\:+\:\mathrm{x}\:+\:\mathrm{x}^{\mathrm{2}} \:+\:…\:\mathrm{x}^{\mathrm{49}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}^{\mathrm{49}} \:−\:\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x} \\ $$
Commented by prakash jain last updated on 01/May/17
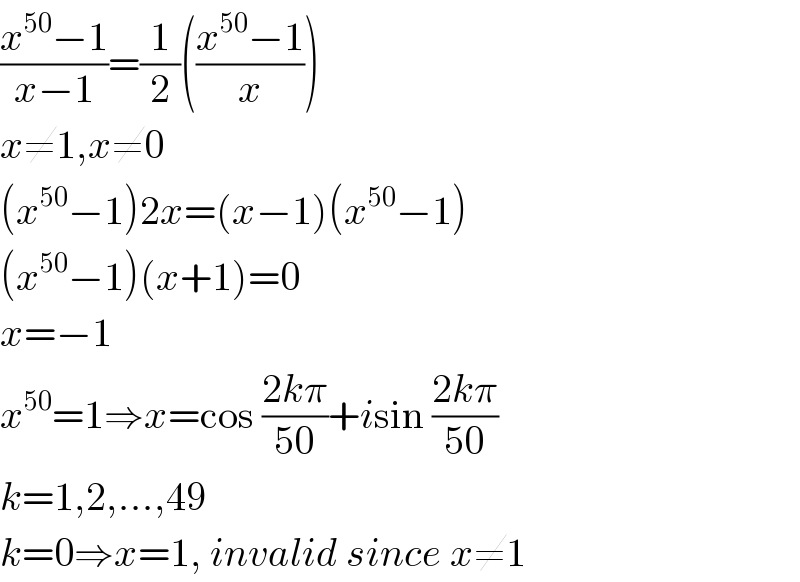
$$\frac{{x}^{\mathrm{50}} −\mathrm{1}}{{x}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}^{\mathrm{50}} −\mathrm{1}}{{x}}\right) \\ $$$${x}\neq\mathrm{1},{x}\neq\mathrm{0} \\ $$$$\left({x}^{\mathrm{50}} −\mathrm{1}\right)\mathrm{2}{x}=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{50}} −\mathrm{1}\right) \\ $$$$\left({x}^{\mathrm{50}} −\mathrm{1}\right)\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{1} \\ $$$${x}^{\mathrm{50}} =\mathrm{1}\Rightarrow{x}=\mathrm{cos}\:\frac{\mathrm{2}{k}\pi}{\mathrm{50}}+{i}\mathrm{sin}\:\frac{\mathrm{2}{k}\pi}{\mathrm{50}}\: \\ $$$${k}=\mathrm{1},\mathrm{2},…,\mathrm{49} \\ $$$${k}=\mathrm{0}\Rightarrow{x}=\mathrm{1},\:{invalid}\:{since}\:{x}\neq\mathrm{1} \\ $$
Commented by tawa last updated on 01/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/May/17
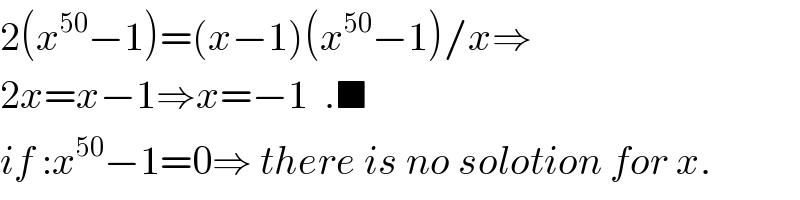
$$\mathrm{2}\left({x}^{\mathrm{50}} −\mathrm{1}\right)=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{50}} −\mathrm{1}\right)/{x}\Rightarrow \\ $$$$\mathrm{2}{x}={x}−\mathrm{1}\Rightarrow{x}=−\mathrm{1}\:\:.\blacksquare \\ $$$${if}\::{x}^{\mathrm{50}} −\mathrm{1}=\mathrm{0}\Rightarrow\:{there}\:{is}\:{no}\:{solotion}\:{for}\:{x}. \\ $$
Commented by tawa last updated on 01/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
