Question Number 70914 by 20190927 last updated on 09/Oct/19
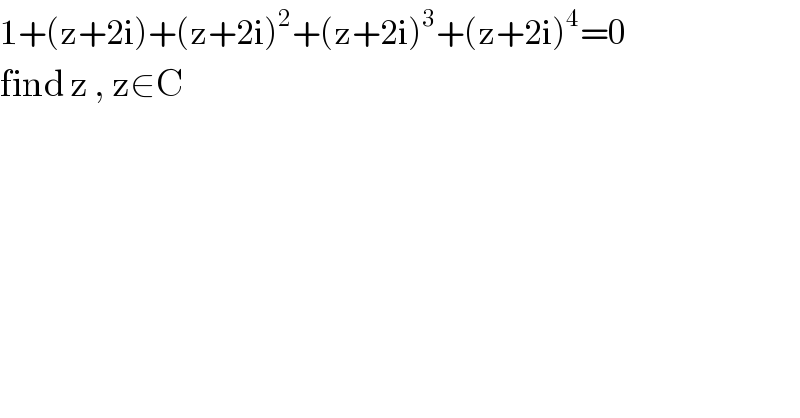
$$\mathrm{1}+\left(\mathrm{z}+\mathrm{2i}\right)+\left(\mathrm{z}+\mathrm{2i}\right)^{\mathrm{2}} +\left(\mathrm{z}+\mathrm{2i}\right)^{\mathrm{3}} +\left(\mathrm{z}+\mathrm{2i}\right)^{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{find}\:\mathrm{z}\:,\:\mathrm{z}\in\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 09/Oct/19
![let x=z+2i (e) ⇔1+x+x^2 +x^3 +x^4 =0 ⇒((1−x^5 )/(1−x)) =0 and x≠1 ⇒ x^5 =1 and x≠1 butx^5 =1 ⇒x^5 =e^(i2kπ) ⇒x_k =e^((i2kπ)/5) and k∈[[1,4]] so the roots of (e) are z_k =x_k −2i z_k =e^((i2kπ)/5) −2i =cos(((2kπ)/5))+i(sin(((2kπ)/5))−2)=r_k e^(iθ_k ) with r_k =(√(cos(((2kπ)/5))^2 +(sin(((2kπ)/5))−2)^2 )) and θ_k =arctan{((sin(((2kπ)/5))−2)/(cos(((2kπ)/5))))} 1≤k≤4](https://www.tinkutara.com/question/Q70929.png)
$${let}\:{x}={z}+\mathrm{2}{i}\:\:\left({e}\right)\:\Leftrightarrow\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} =\mathrm{0}\:\Rightarrow\frac{\mathrm{1}−{x}^{\mathrm{5}} }{\mathrm{1}−{x}}\:=\mathrm{0}\:{and}\:{x}\neq\mathrm{1}\:\Rightarrow \\ $$$${x}^{\mathrm{5}} =\mathrm{1}\:{and}\:{x}\neq\mathrm{1}\:\:{butx}^{\mathrm{5}} =\mathrm{1}\:\Rightarrow{x}^{\mathrm{5}} ={e}^{{i}\mathrm{2}{k}\pi} \:\Rightarrow{x}_{{k}} ={e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{5}}} \\ $$$${and}\:{k}\in\left[\left[\mathrm{1},\mathrm{4}\right]\right]\:{so}\:{the}\:{roots}\:{of}\:\left({e}\right)\:{are}\:{z}_{{k}} ={x}_{{k}} −\mathrm{2}{i} \\ $$$${z}_{{k}} ={e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{5}}} −\mathrm{2}{i}\:\:={cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right)+{i}\left({sin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right)−\mathrm{2}\right)={r}_{{k}} {e}^{{i}\theta_{{k}} } \\ $$$${with}\:{r}_{{k}} =\sqrt{{cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right)^{\mathrm{2}} \:+\left({sin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right)−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${and}\:\theta_{{k}} ={arctan}\left\{\frac{{sin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right)−\mathrm{2}}{{cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\right)}\right\}\:\:\:\mathrm{1}\leqslant{k}\leqslant\mathrm{4} \\ $$
Commented by 20190927 last updated on 10/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathmax by abdo last updated on 10/Oct/19
$${you}\:{are}\:{welcome}. \\ $$
Answered by mind is power last updated on 09/Oct/19
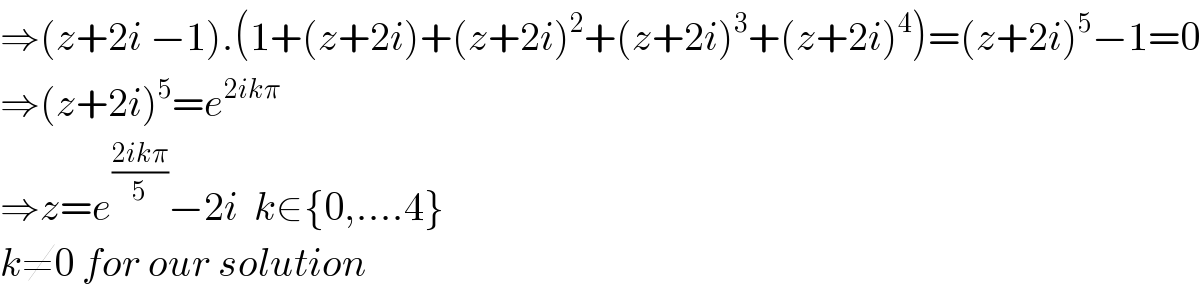
$$\Rightarrow\left({z}+\mathrm{2}{i}\:−\mathrm{1}\right).\left(\mathrm{1}+\left({z}+\mathrm{2}{i}\right)+\left({z}+\mathrm{2}{i}\right)^{\mathrm{2}} +\left({z}+\mathrm{2}{i}\right)^{\mathrm{3}} +\left({z}+\mathrm{2}{i}\right)^{\mathrm{4}} \right)=\left({z}+\mathrm{2}{i}\right)^{\mathrm{5}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left({z}+\mathrm{2}{i}\right)^{\mathrm{5}} ={e}^{\mathrm{2}{ik}\pi} \\ $$$$\Rightarrow{z}={e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{5}}} −\mathrm{2}{i}\:\:{k}\in\left\{\mathrm{0},….\mathrm{4}\right\} \\ $$$${k}\neq\mathrm{0}\:{for}\:{our}\:{solution} \\ $$
Commented by 20190927 last updated on 10/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mind is power last updated on 10/Oct/19

$${y}'{re}\:{welcom} \\ $$
Answered by MJS last updated on 09/Oct/19
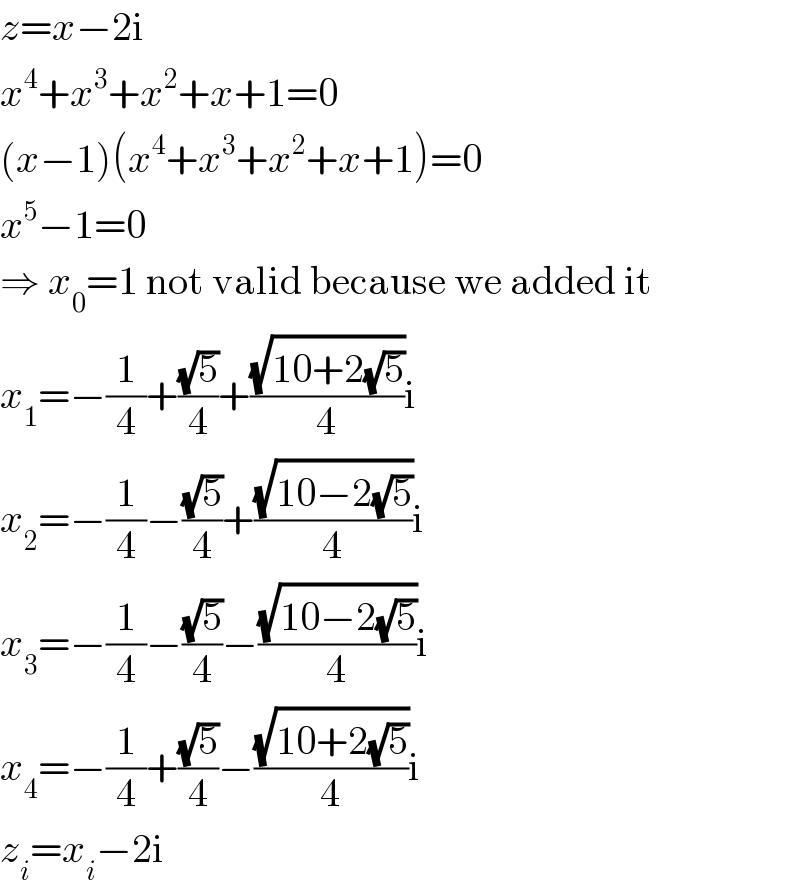
$${z}={x}−\mathrm{2i} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{5}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{x}_{\mathrm{0}} =\mathrm{1}\:\mathrm{not}\:\mathrm{valid}\:\mathrm{because}\:\mathrm{we}\:\mathrm{added}\:\mathrm{it} \\ $$$${x}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\mathrm{i} \\ $$$${x}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\mathrm{i} \\ $$$${x}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}−\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\mathrm{i} \\ $$$${x}_{\mathrm{4}} =−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}−\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\mathrm{i} \\ $$$${z}_{{i}} ={x}_{{i}} −\mathrm{2i} \\ $$
Commented by 20190927 last updated on 10/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
