Menu Close

10-3-11-3-12-3-20-3-Is-there-any-ways-to-count-the-sum-of-that-sequence-without-sum-them-manually-

Tinku Tara 0 Comments
Pin




Question Number 12107 by Joel576 last updated on 13/Apr/17
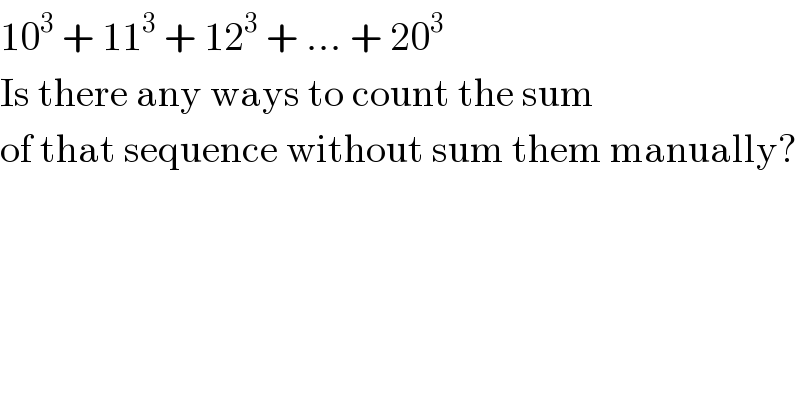
10^3 + 11^3 + 12^3 + ... + 20^3 Is there any ways to count the sum of that sequence without sum them manually?
$$\mathrm{10}^{\mathrm{3}} \:+\:\mathrm{11}^{\mathrm{3}} \:+\:\mathrm{12}^{\mathrm{3}} \:+\:…\:+\:\mathrm{20}^{\mathrm{3}} \\ $$$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{count}\:\mathrm{the}\:\mathrm{sum}\: \\ $$$$\mathrm{of}\:\mathrm{that}\:\mathrm{sequence}\:\mathrm{without}\:\mathrm{sum}\:\mathrm{them}\:\mathrm{manually}? \\ $$
Commented by FilupS last updated on 13/Apr/17
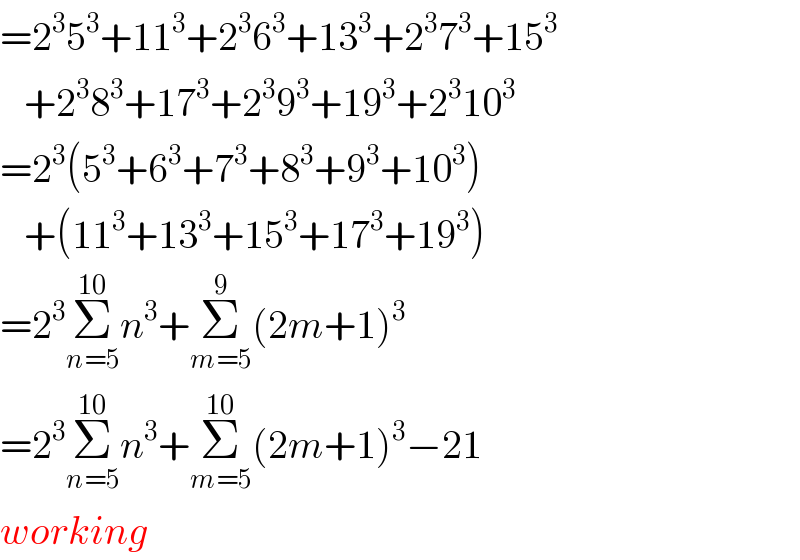
=2^3 5^3 +11^3 +2^3 6^3 +13^3 +2^3 7^3 +15^3 +2^3 8^3 +17^3 +2^3 9^3 +19^3 +2^3 10^3 =2^3 (5^3 +6^3 +7^3 +8^3 +9^3 +10^3 ) +(11^3 +13^3 +15^3 +17^3 +19^3 ) =2^3 Σ_(n=5) ^(10) n^3 +Σ_(m=5) ^9 (2m+1)^3 =2^3 Σ_(n=5) ^(10) n^3 +Σ_(m=5) ^(10) (2m+1)^3 −21 working
$$=\mathrm{2}^{\mathrm{3}} \mathrm{5}^{\mathrm{3}} +\mathrm{11}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} \mathrm{6}^{\mathrm{3}} +\mathrm{13}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} \mathrm{7}^{\mathrm{3}} +\mathrm{15}^{\mathrm{3}} \\ $$$$\:\:\:+\mathrm{2}^{\mathrm{3}} \mathrm{8}^{\mathrm{3}} +\mathrm{17}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} \mathrm{9}^{\mathrm{3}} +\mathrm{19}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} \mathrm{10}^{\mathrm{3}} \\ $$$$=\mathrm{2}^{\mathrm{3}} \left(\mathrm{5}^{\mathrm{3}} +\mathrm{6}^{\mathrm{3}} +\mathrm{7}^{\mathrm{3}} +\mathrm{8}^{\mathrm{3}} +\mathrm{9}^{\mathrm{3}} +\mathrm{10}^{\mathrm{3}} \right) \\ $$$$\:\:\:+\left(\mathrm{11}^{\mathrm{3}} +\mathrm{13}^{\mathrm{3}} +\mathrm{15}^{\mathrm{3}} +\mathrm{17}^{\mathrm{3}} +\mathrm{19}^{\mathrm{3}} \right) \\ $$$$=\mathrm{2}^{\mathrm{3}} \underset{{n}=\mathrm{5}} {\overset{\mathrm{10}} {\sum}}{n}^{\mathrm{3}} +\underset{{m}=\mathrm{5}} {\overset{\mathrm{9}} {\sum}}\left(\mathrm{2}{m}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$=\mathrm{2}^{\mathrm{3}} \underset{{n}=\mathrm{5}} {\overset{\mathrm{10}} {\sum}}{n}^{\mathrm{3}} +\underset{{m}=\mathrm{5}} {\overset{\mathrm{10}} {\sum}}\left(\mathrm{2}{m}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{21} \\ $$$${working} \\ $$
Commented by Joel576 last updated on 14/Apr/17
but how to count [Σ_(m=5) ^(10) (2m + 1)^3 ] − 21^3 without adding them manually?
$$\mathrm{but}\:\mathrm{how}\:\mathrm{to}\:\mathrm{count}\:\left[\underset{{m}=\mathrm{5}} {\overset{\mathrm{10}} {\sum}}\left(\mathrm{2}{m}\:+\:\mathrm{1}\right)^{\mathrm{3}} \right]\:−\:\mathrm{21}^{\mathrm{3}} \\ $$$$\mathrm{without}\:\mathrm{adding}\:\mathrm{them}\:\mathrm{manually}? \\ $$
Answered by mrW1 last updated on 13/Apr/17
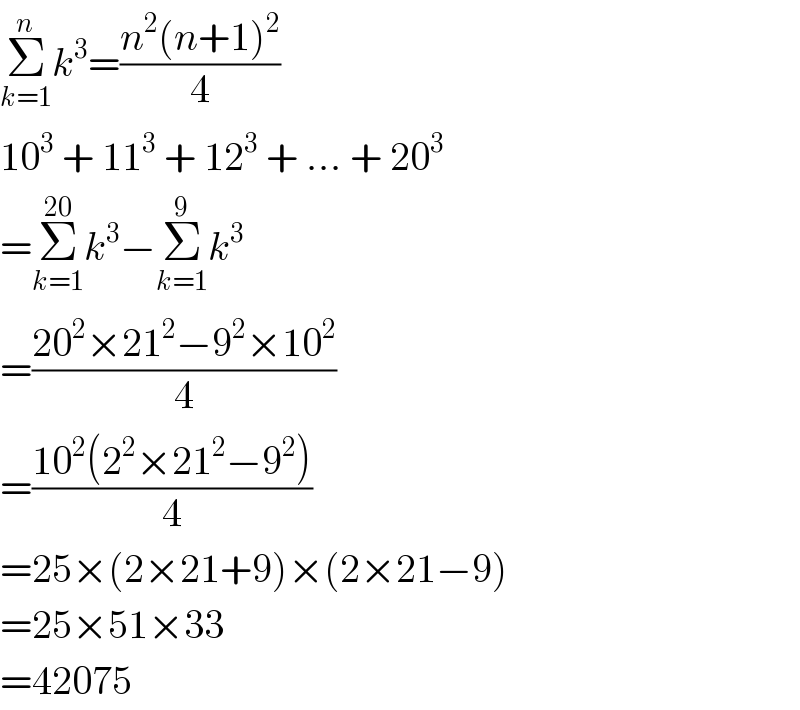
Σ_(k=1) ^n k^3 =((n^2 (n+1)^2 )/4) 10^3 + 11^3 + 12^3 + ... + 20^3 =Σ_(k=1) ^(20) k^3 −Σ_(k=1) ^9 k^3 =((20^2 ×21^2 −9^2 ×10^2 )/4) =((10^2 (2^2 ×21^2 −9^2 ))/4) =25×(2×21+9)×(2×21−9) =25×51×33 =42075
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{3}} =\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{10}^{\mathrm{3}} \:+\:\mathrm{11}^{\mathrm{3}} \:+\:\mathrm{12}^{\mathrm{3}} \:+\:…\:+\:\mathrm{20}^{\mathrm{3}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}{k}^{\mathrm{3}} −\underset{{k}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}{k}^{\mathrm{3}} \\ $$$$=\frac{\mathrm{20}^{\mathrm{2}} ×\mathrm{21}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} ×\mathrm{10}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\frac{\mathrm{10}^{\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}} ×\mathrm{21}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} \right)}{\mathrm{4}} \\ $$$$=\mathrm{25}×\left(\mathrm{2}×\mathrm{21}+\mathrm{9}\right)×\left(\mathrm{2}×\mathrm{21}−\mathrm{9}\right) \\ $$$$=\mathrm{25}×\mathrm{51}×\mathrm{33} \\ $$$$=\mathrm{42075} \\ $$
Commented by Joel576 last updated on 14/Apr/17
thank you very much
$${thank}\:{you}\:{very}\:{much} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *