Question Number 136123 by bramlexs22 last updated on 18/Mar/21
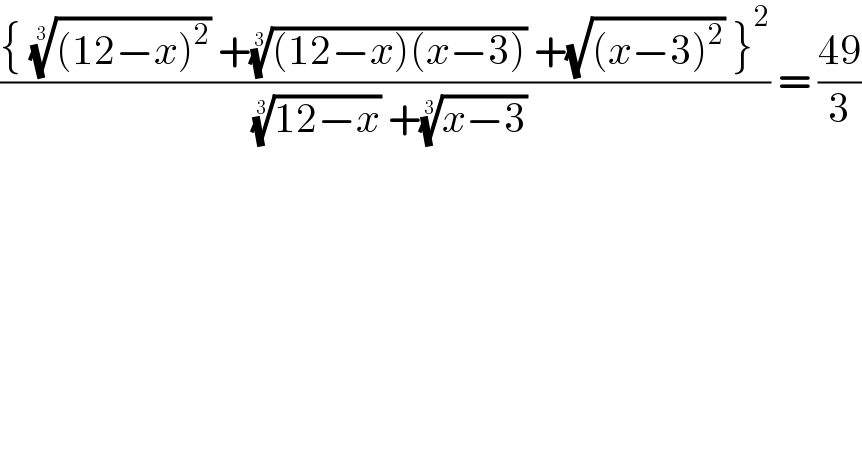
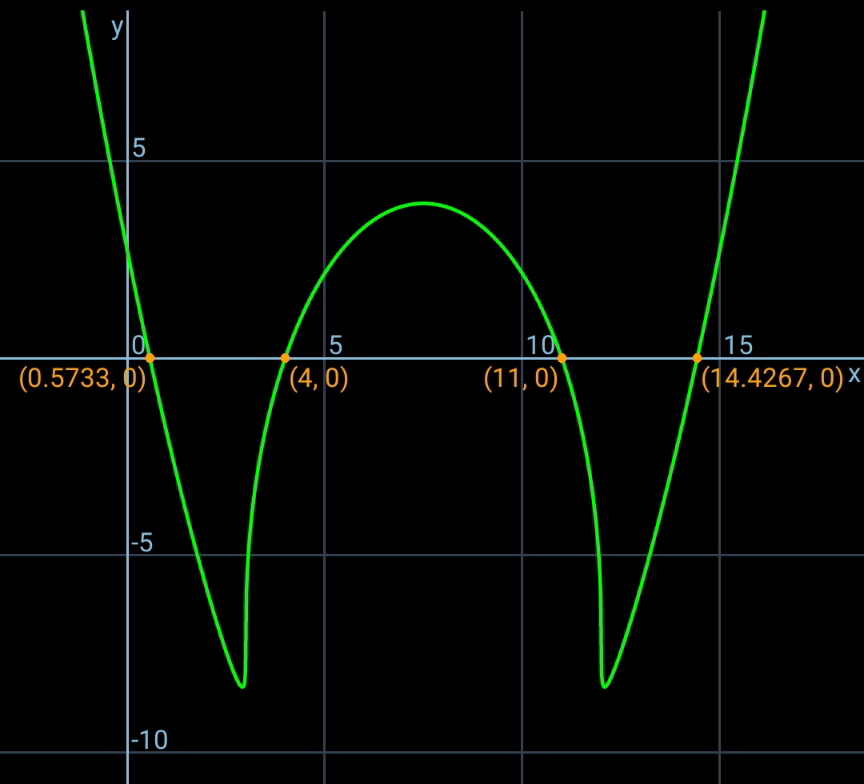
$$\frac{\left\{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{12}−{x}\right)^{\mathrm{2}} }\:+\sqrt[{\mathrm{3}}]{\left(\mathrm{12}−{x}\right)\left({x}−\mathrm{3}\right)}\:+\sqrt{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:\right\}^{\mathrm{2}} }{\:\sqrt[{\mathrm{3}}]{\mathrm{12}−{x}}\:+\sqrt[{\mathrm{3}}]{{x}−\mathrm{3}}}\:=\:\frac{\mathrm{49}}{\mathrm{3}} \\ $$
Answered by EDWIN88 last updated on 19/Mar/21
![let (((12−x)))^(1/3) = p & ((x−3))^(1/3) = q ⇒ (((p^2 +pq+q^2 )^2 )/(p+q)) = ((49)/3) ⇒3[ (p+q)^2 −pq ]^2 = 49(p+q)](https://www.tinkutara.com/question/Q136128.png)
$$\mathrm{let}\:\sqrt[{\mathrm{3}}]{\left(\mathrm{12}−\mathrm{x}\right)}\:=\:\mathrm{p}\:\&\:\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{3}}\:=\:\mathrm{q} \\ $$$$\Rightarrow\:\frac{\left(\mathrm{p}^{\mathrm{2}} +\mathrm{pq}+\mathrm{q}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{p}+\mathrm{q}}\:=\:\frac{\mathrm{49}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{3}\left[\:\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} −\mathrm{pq}\:\right]^{\mathrm{2}} =\:\mathrm{49}\left(\mathrm{p}+\mathrm{q}\right) \\ $$$$ \\ $$
Answered by MJS_new last updated on 19/Mar/21

$${x}=\mathrm{4}\vee{x}=\mathrm{11} \\ $$
Commented by bramlexs22 last updated on 19/Mar/21

$${step}\:{by}\:{step}\:{sir} \\ $$
Commented by MJS_new last updated on 19/Mar/21
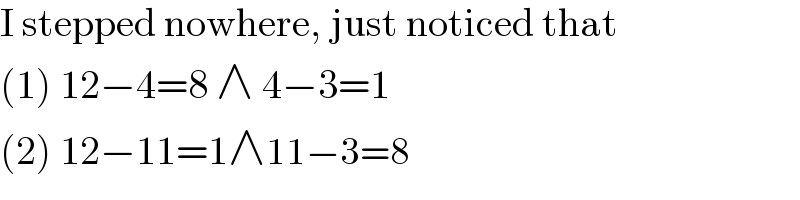
$$\mathrm{I}\:\mathrm{stepped}\:\mathrm{nowhere},\:\mathrm{just}\:\mathrm{noticed}\:\mathrm{that} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{12}−\mathrm{4}=\mathrm{8}\:\wedge\:\mathrm{4}−\mathrm{3}=\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{12}−\mathrm{11}=\mathrm{1}\wedge\mathrm{11}−\mathrm{3}=\mathrm{8} \\ $$
Answered by mr W last updated on 19/Mar/21
![let a=((12−x))^(1/3) , b=((x−3))^(1/3) a^3 =12−x b^3 =x−3 ⇒a^3 +b^3 =9 ⇒(a+b)(a^2 +b^2 −ab)=9 ⇒(a+b)((a+b)^2 −3ab)=9 let u=a+b, v=ab ⇒u(u^2 −3v)=9 ...(i) given: (((a^2 +ab+b^2 )^2 )/(a+b))=((49)/3) ((a+b)^2 −ab)^2 =((49(a+b))/3) ⇒(u^2 −v)^2 =((49u)/3) ...(ii) from (i): u[3(u^2 −v)−2u^2 ]=9 ⇒u^2 −v=(1/3)(2u^2 +(9/u))=((2u^3 +9)/(3u)) inserting into (ii): (((2u^3 +9)/(3u)))^2 =((49u)/3) 4u^6 +36u^3 +81=147u^3 4u^6 −111u^3 +81=0 u^3 =((111±(√(111^2 −4×4×81)))/(2×4))=(3/4) or 27 ⇒u=((3/4))^(1/3) or ((27))^(1/3) = 3 v=u^2 −((2u^3 +9)/(3u))=(u^2 /3)−(3/u)=−((11((36))^(1/3) )/(12)) or 2 since a+b=u, ab=v a and b are roots of z^2 −uz+v=0 ⇒a,b=z=((u±(√(u^2 −4v)))/2)=(u/2)(1±(√(((12)/u^3 )−(1/3)))) from a=((12−x))^(1/3) ⇒x=12−a^3 =12−(u^3 /8)(1±(√(((12)/u^3 )−(1/3))))^3 with u^3 =(3/4): x=12−(3/(32))(1±(√(((12×4)/3)−(1/3))))^3 =12−(3/(32))(1±(√((47)/3)))^3 =((15)/2)±((7(√(141)))/(12)) ≈0.573 300 449 or ≈14.426 699 551 with u^3 =27: x=12−((27)/8)(1±(√(((12)/(27))−(1/3))))^3 =12−((27)/8)(1±(1/3))^3 =4 or 11](https://www.tinkutara.com/question/Q136158.png)
$${let}\:{a}=\sqrt[{\mathrm{3}}]{\mathrm{12}−{x}},\:{b}=\sqrt[{\mathrm{3}}]{{x}−\mathrm{3}} \\ $$$${a}^{\mathrm{3}} =\mathrm{12}−{x} \\ $$$${b}^{\mathrm{3}} ={x}−\mathrm{3} \\ $$$$\Rightarrow{a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\mathrm{9} \\ $$$$\Rightarrow\left({a}+{b}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)=\mathrm{9} \\ $$$$\Rightarrow\left({a}+{b}\right)\left(\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{3}{ab}\right)=\mathrm{9} \\ $$$${let}\:{u}={a}+{b},\:{v}={ab} \\ $$$$\Rightarrow{u}\left({u}^{\mathrm{2}} −\mathrm{3}{v}\right)=\mathrm{9}\:\:\:…\left({i}\right) \\ $$$${given}: \\ $$$$\frac{\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{{a}+{b}}=\frac{\mathrm{49}}{\mathrm{3}} \\ $$$$\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)^{\mathrm{2}} =\frac{\mathrm{49}\left({a}+{b}\right)}{\mathrm{3}} \\ $$$$\Rightarrow\left({u}^{\mathrm{2}} −{v}\right)^{\mathrm{2}} =\frac{\mathrm{49}{u}}{\mathrm{3}}\:\:\:…\left({ii}\right) \\ $$$${from}\:\left({i}\right): \\ $$$${u}\left[\mathrm{3}\left({u}^{\mathrm{2}} −{v}\right)−\mathrm{2}{u}^{\mathrm{2}} \right]=\mathrm{9} \\ $$$$\Rightarrow{u}^{\mathrm{2}} −{v}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}{u}^{\mathrm{2}} +\frac{\mathrm{9}}{{u}}\right)=\frac{\mathrm{2}{u}^{\mathrm{3}} +\mathrm{9}}{\mathrm{3}{u}} \\ $$$${inserting}\:{into}\:\left({ii}\right): \\ $$$$\left(\frac{\mathrm{2}{u}^{\mathrm{3}} +\mathrm{9}}{\mathrm{3}{u}}\right)^{\mathrm{2}} =\frac{\mathrm{49}{u}}{\mathrm{3}} \\ $$$$\mathrm{4}{u}^{\mathrm{6}} +\mathrm{36}{u}^{\mathrm{3}} +\mathrm{81}=\mathrm{147}{u}^{\mathrm{3}} \\ $$$$\mathrm{4}{u}^{\mathrm{6}} −\mathrm{111}{u}^{\mathrm{3}} +\mathrm{81}=\mathrm{0} \\ $$$${u}^{\mathrm{3}} =\frac{\mathrm{111}\pm\sqrt{\mathrm{111}^{\mathrm{2}} −\mathrm{4}×\mathrm{4}×\mathrm{81}}}{\mathrm{2}×\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{4}}\:{or}\:\mathrm{27} \\ $$$$\Rightarrow{u}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{3}}{\mathrm{4}}}\:{or}\:\sqrt[{\mathrm{3}}]{\mathrm{27}}=\:\mathrm{3} \\ $$$${v}={u}^{\mathrm{2}} −\frac{\mathrm{2}{u}^{\mathrm{3}} +\mathrm{9}}{\mathrm{3}{u}}=\frac{{u}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{3}}{{u}}=−\frac{\mathrm{11}\sqrt[{\mathrm{3}}]{\mathrm{36}}}{\mathrm{12}}\:{or}\:\mathrm{2} \\ $$$${since}\:{a}+{b}={u},\:{ab}={v} \\ $$$${a}\:{and}\:{b}\:{are}\:{roots}\:{of} \\ $$$${z}^{\mathrm{2}} −{uz}+{v}=\mathrm{0} \\ $$$$\Rightarrow{a},{b}={z}=\frac{{u}\pm\sqrt{{u}^{\mathrm{2}} −\mathrm{4}{v}}}{\mathrm{2}}=\frac{{u}}{\mathrm{2}}\left(\mathrm{1}\pm\sqrt{\frac{\mathrm{12}}{{u}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{3}}}\right) \\ $$$${from}\:{a}=\sqrt[{\mathrm{3}}]{\mathrm{12}−{x}} \\ $$$$\Rightarrow{x}=\mathrm{12}−{a}^{\mathrm{3}} =\mathrm{12}−\frac{{u}^{\mathrm{3}} }{\mathrm{8}}\left(\mathrm{1}\pm\sqrt{\frac{\mathrm{12}}{{u}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{3}}}\right)^{\mathrm{3}} \\ $$$${with}\:{u}^{\mathrm{3}} =\frac{\mathrm{3}}{\mathrm{4}}: \\ $$$${x}=\mathrm{12}−\frac{\mathrm{3}}{\mathrm{32}}\left(\mathrm{1}\pm\sqrt{\frac{\mathrm{12}×\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}}\right)^{\mathrm{3}} \\ $$$$\:\:\:=\mathrm{12}−\frac{\mathrm{3}}{\mathrm{32}}\left(\mathrm{1}\pm\sqrt{\frac{\mathrm{47}}{\mathrm{3}}}\right)^{\mathrm{3}} \\ $$$$\: \\ $$$$\:\:=\frac{\mathrm{15}}{\mathrm{2}}\pm\frac{\mathrm{7}\sqrt{\mathrm{141}}}{\mathrm{12}} \\ $$$$\:\:\approx\mathrm{0}.\mathrm{573}\:\mathrm{300}\:\mathrm{449} \\ $$$$\:\:\:{or} \\ $$$$\:\:\approx\mathrm{14}.\mathrm{426}\:\mathrm{699}\:\mathrm{551} \\ $$$$ \\ $$$${with}\:{u}^{\mathrm{3}} =\mathrm{27}: \\ $$$${x}=\mathrm{12}−\frac{\mathrm{27}}{\mathrm{8}}\left(\mathrm{1}\pm\sqrt{\frac{\mathrm{12}}{\mathrm{27}}−\frac{\mathrm{1}}{\mathrm{3}}}\right)^{\mathrm{3}} \\ $$$$\:\:=\mathrm{12}−\frac{\mathrm{27}}{\mathrm{8}}\left(\mathrm{1}\pm\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$\:\:=\mathrm{4}\:{or}\:\mathrm{11} \\ $$
Commented by mr W last updated on 19/Mar/21