Question Number 70021 by naka3546 last updated on 30/Sep/19

$$\sqrt[{\mathrm{3}}]{\sqrt{\sqrt{\mathrm{12345689654321233}\:+\:\mathrm{5333334096}\:\sqrt{\mathrm{12345679}}}}\:−\:\sqrt{\sqrt{\mathrm{12345689654321233}\:−\:\mathrm{5333334096}\:\sqrt{\mathrm{12345679}}}}}\:\:=\:\:… \\ $$
Commented by MJS last updated on 30/Sep/19
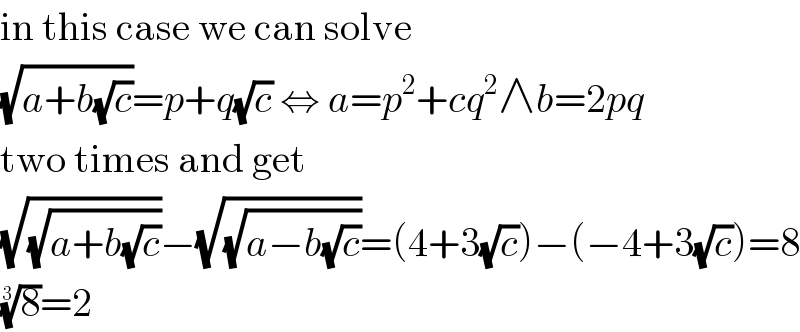
$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve} \\ $$$$\sqrt{{a}+{b}\sqrt{{c}}}={p}+{q}\sqrt{{c}}\:\Leftrightarrow\:{a}={p}^{\mathrm{2}} +{cq}^{\mathrm{2}} \wedge{b}=\mathrm{2}{pq} \\ $$$$\mathrm{two}\:\mathrm{times}\:\mathrm{and}\:\mathrm{get} \\ $$$$\sqrt{\sqrt{{a}+{b}\sqrt{{c}}}}−\sqrt{\sqrt{{a}−{b}\sqrt{{c}}}}=\left(\mathrm{4}+\mathrm{3}\sqrt{{c}}\right)−\left(−\mathrm{4}+\mathrm{3}\sqrt{{c}}\right)=\mathrm{8} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{8}}=\mathrm{2} \\ $$
Commented by ajfour last updated on 30/Sep/19
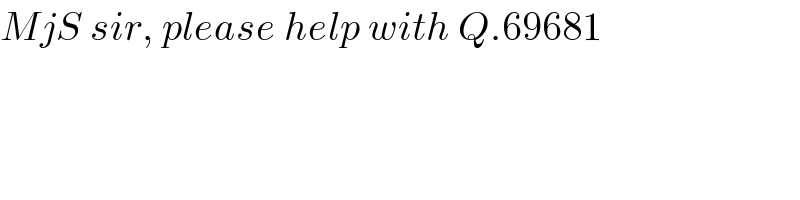
$${MjS}\:{sir},\:{please}\:{help}\:{with}\:{Q}.\mathrm{69681} \\ $$
