Question Number 5026 by gourav~ last updated on 04/Apr/16
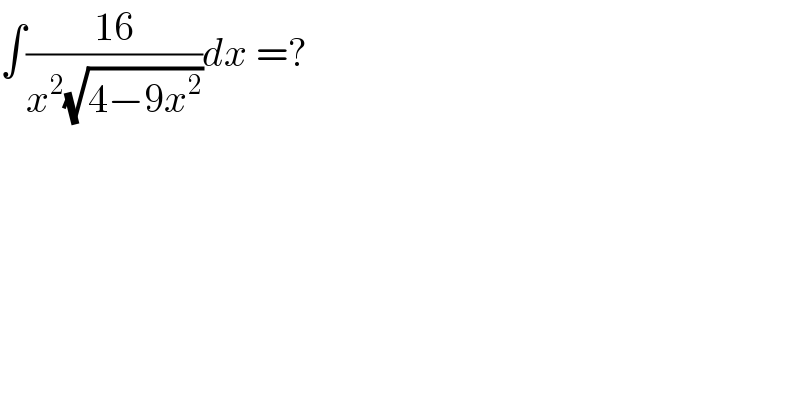
$$\int\frac{\mathrm{16}}{{x}^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }}{dx}\:=? \\ $$$$ \\ $$
Answered by Yozzii last updated on 04/Apr/16

$${Let}\:{x}=\frac{\mathrm{2}}{\mathrm{3}}{cosy}\Rightarrow{dx}=−\frac{\mathrm{2}}{\mathrm{3}}{sinydy} \\ $$$$\sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }=\sqrt{\mathrm{4}−\mathrm{9}×\frac{\mathrm{4}}{\mathrm{9}}{cos}^{\mathrm{2}} {y}}=\mathrm{2}{siny}. \\ $$$${cosy}=\frac{\mathrm{3}{x}}{\mathrm{2}}\Rightarrow{siny}=\frac{\sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\therefore\:\int\frac{\mathrm{16}}{{x}^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }}{dx}=\int\frac{−\mathrm{16}×\frac{\mathrm{2}}{\mathrm{3}}{siny}}{\frac{\mathrm{4}}{\mathrm{9}}{cos}^{\mathrm{2}} {y}×\mathrm{2}{siny}}{dy} \\ $$$$=−\mathrm{12}\int{sec}^{\mathrm{2}} {ydy} \\ $$$$=−\mathrm{12}{tany}+{c} \\ $$$$=−\mathrm{12}\frac{\sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }}{\mathrm{3}{x}}+{c} \\ $$$$\int\frac{\mathrm{16}}{{x}^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }}{dx}=\frac{−\mathrm{4}\sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }}{{x}}+{c} \\ $$$${c}={constant}. \\ $$
