Menu Close

16x-2-25-dx-

Tinku Tara 0 Comments
Pin




Question Number 5065 by gourav~ last updated on 07/Apr/16
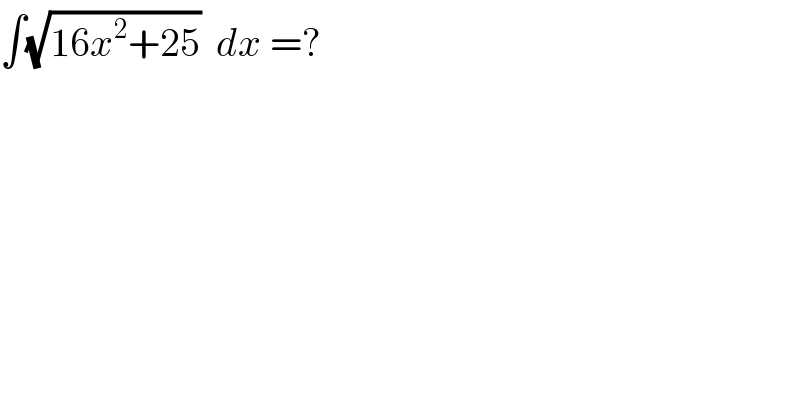
∫(√(16x^2 +25)) dx =?
$$\int\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}\:\:{dx}\:=? \\ $$
Answered by Yozzii last updated on 08/Apr/16
Let x=(5/4)sinhθ⇒dx=(5/4)coshθdθ (√(16x^2 +25))=(√(16×((25)/(16))sinh^2 θ+25)) =5(√(1+sinh^2 θ))=5coshθ {cosh^2 θ=1+sinh^2 θ} ∴ ∫(√(16x^2 +25))dx=∫((25)/4)cosh^2 θdθ =((25)/4)∫(1/2)(1+cosh2θ)dθ {cosh2θ=2cosh^2 θ−1} =((25)/8)(θ+(1/2)sinh2θ)+C {(d/dθ)sinh(aθ)=acosh(aθ)} But, θ=sinh^(−1) (((4x)/5))=ln(((4x)/5)+(√(((16x^2 )/(25))+1)))=ln(4x+(√(16x^2 +25)))−ln5 {sinh^(−1) ax=ln(ax+(√(a^2 x^2 +1)))} (1/2)sinh2θ=sinhθcoshθ=((4xcoshθ)/5) ∴ ∫(√(16x^2 +25))dx=((25)/8)(ln(4x+(√(16x^2 +25)))+((4x)/5)cosh{ln(((4x)/5)+(√(((16x^2 )/(25))+1)))})+K ∫(√(16x^2 +25))dx=((25)/8)ln(4x+(√(16x^2 +25)))+(({4x+(√(16x^2 +25))}^2 +25)/(4{4x+(√(16x^2 +25))}))x+K K=constant of integration {K=C−((25)/8)ln5}
$${Let}\:{x}=\frac{\mathrm{5}}{\mathrm{4}}{sinh}\theta\Rightarrow{dx}=\frac{\mathrm{5}}{\mathrm{4}}{cosh}\theta{d}\theta \\ $$$$\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}=\sqrt{\mathrm{16}×\frac{\mathrm{25}}{\mathrm{16}}{sinh}^{\mathrm{2}} \theta+\mathrm{25}} \\ $$$$=\mathrm{5}\sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} \theta}=\mathrm{5}{cosh}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{cosh}^{\mathrm{2}} \theta=\mathrm{1}+{sinh}^{\mathrm{2}} \theta\right\} \\ $$$$\therefore\:\int\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}{dx}=\int\frac{\mathrm{25}}{\mathrm{4}}{cosh}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\frac{\mathrm{25}}{\mathrm{4}}\int\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{cosh}\mathrm{2}\theta\right){d}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{cosh}\mathrm{2}\theta=\mathrm{2}{cosh}^{\mathrm{2}} \theta−\mathrm{1}\right\} \\ $$$$=\frac{\mathrm{25}}{\mathrm{8}}\left(\theta+\frac{\mathrm{1}}{\mathrm{2}}{sinh}\mathrm{2}\theta\right)+{C}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\frac{{d}}{{d}\theta}{sinh}\left({a}\theta\right)={acosh}\left({a}\theta\right)\right\} \\ $$$${But},\:\theta={sinh}^{−\mathrm{1}} \left(\frac{\mathrm{4}{x}}{\mathrm{5}}\right)={ln}\left(\frac{\mathrm{4}{x}}{\mathrm{5}}+\sqrt{\frac{\mathrm{16}{x}^{\mathrm{2}} }{\mathrm{25}}+\mathrm{1}}\right)={ln}\left(\mathrm{4}{x}+\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}\right)−{ln}\mathrm{5} \\ $$$$\left\{{sinh}^{−\mathrm{1}} {ax}={ln}\left({ax}+\sqrt{{a}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{1}}\right)\right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{sinh}\mathrm{2}\theta={sinh}\theta{cosh}\theta=\frac{\mathrm{4}{xcosh}\theta}{\mathrm{5}} \\ $$$$\therefore\:\int\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}{dx}=\frac{\mathrm{25}}{\mathrm{8}}\left({ln}\left(\mathrm{4}{x}+\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}\right)+\frac{\mathrm{4}{x}}{\mathrm{5}}{cosh}\left\{{ln}\left(\frac{\mathrm{4}{x}}{\mathrm{5}}+\sqrt{\frac{\mathrm{16}{x}^{\mathrm{2}} }{\mathrm{25}}+\mathrm{1}}\right)\right\}\right)+{K} \\ $$$$\int\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}{dx}=\frac{\mathrm{25}}{\mathrm{8}}{ln}\left(\mathrm{4}{x}+\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}\right)+\frac{\left\{\mathrm{4}{x}+\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}\right\}^{\mathrm{2}} +\mathrm{25}}{\mathrm{4}\left\{\mathrm{4}{x}+\sqrt{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{25}}\right\}}{x}+{K} \\ $$$${K}={constant}\:{of}\:{integration} \\ $$$$\left\{{K}={C}−\frac{\mathrm{25}}{\mathrm{8}}{ln}\mathrm{5}\right\} \\ $$$$ \\ $$
Commented by Yozzii last updated on 08/Apr/16
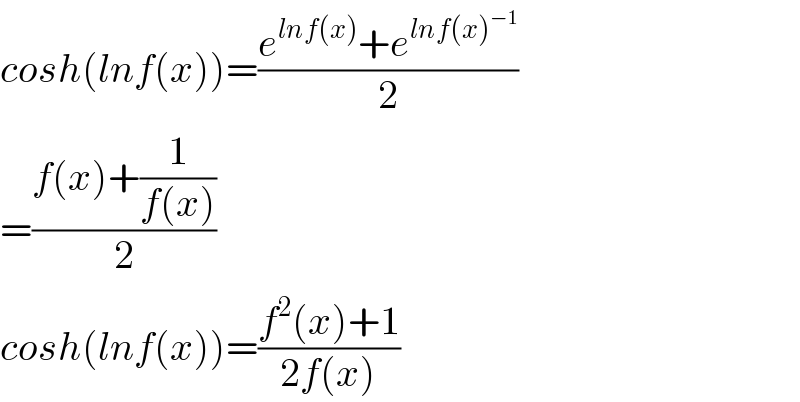
cosh(lnf(x))=((e^(lnf(x)) +e^(lnf(x)^(−1) ) )/2) =((f(x)+(1/(f(x))))/2) cosh(lnf(x))=((f^2 (x)+1)/(2f(x)))
$${cosh}\left({lnf}\left({x}\right)\right)=\frac{{e}^{{lnf}\left({x}\right)} +{e}^{{lnf}\left({x}\right)^{−\mathrm{1}} } }{\mathrm{2}} \\ $$$$=\frac{{f}\left({x}\right)+\frac{\mathrm{1}}{{f}\left({x}\right)}}{\mathrm{2}} \\ $$$${cosh}\left({lnf}\left({x}\right)\right)=\frac{{f}^{\mathrm{2}} \left({x}\right)+\mathrm{1}}{\mathrm{2}{f}\left({x}\right)} \\ $$
Commented by Yozzy last updated on 08/Apr/16
Let′s look at solving I=∫(√(ax^2 +b ))dx where a,b∈R^+ . Let x=((√b)/( (√a)))sinhu⇒dx=((√b)/( (√a)))coshudu. (√(ax^2 +b))=(√(a×(b/a)sinh^2 u+b))=(√b)(√(1+sinh^2 u))=(√b)coshu. ∴ I=∫((√b)/( (√a)))×(√b)coshu×coshudu =((b(√a))/a)∫cosh^2 udu =((b(√a))/(2a))∫(1+cosh2u)du =((b(√a))/(2a))(u+(1/2)sinh2u)+C I=((b(√a))/(2a))u+((b(√a))/(4a))sinh2u+C Since x=(√(b/a))sinhu⇒u=sinh^(−1) ((√(a/b))x). But, sinh^(−1) k=ln(k+(√(k^2 +1))) by definition. ∴ u=ln(k+(√(k^2 +1))) where we let k=(√(a/b))x. By definition, sinh2u=((e^(2u) −e^(−2u) )/2). Let u=ln(g(x)) ⇒sinh2u=((e^(2lng(x)) −e^(−2lng(x)) )/2) sinh2u=((g(x)^2 −(1/(g(x)^2 )))/2)=((g(x)^4 −1)/(2g(x)^2 )). For this problem, g(x)=k+(√(k^2 +1)). ⇒I=((b(√a))/(2a))ln(k+(√(k^2 +1)))+((b(√a))/(4a))((((k+(√(k^2 +1)))^4 −1)/(2(k+(√(k^2 +1)))^2 )))+C
$${Let}'{s}\:{look}\:{at}\:{solving}\:{I}=\int\sqrt{{ax}^{\mathrm{2}} +{b}\:}{dx}\:{where}\:{a},{b}\in\mathbb{R}^{+} . \\ $$$${Let}\:{x}=\frac{\sqrt{{b}}}{\:\sqrt{{a}}}{sinhu}\Rightarrow{dx}=\frac{\sqrt{{b}}}{\:\sqrt{{a}}}{coshudu}. \\ $$$$\sqrt{{ax}^{\mathrm{2}} +{b}}=\sqrt{{a}×\frac{{b}}{{a}}{sinh}^{\mathrm{2}} {u}+{b}}=\sqrt{{b}}\sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} {u}}=\sqrt{{b}}{coshu}. \\ $$$$\therefore\:{I}=\int\frac{\sqrt{{b}}}{\:\sqrt{{a}}}×\sqrt{{b}}{coshu}×{coshudu} \\ $$$$=\frac{{b}\sqrt{{a}}}{{a}}\int{cosh}^{\mathrm{2}} {udu} \\ $$$$=\frac{{b}\sqrt{{a}}}{\mathrm{2}{a}}\int\left(\mathrm{1}+{cosh}\mathrm{2}{u}\right){du} \\ $$$$=\frac{{b}\sqrt{{a}}}{\mathrm{2}{a}}\left({u}+\frac{\mathrm{1}}{\mathrm{2}}{sinh}\mathrm{2}{u}\right)+{C} \\ $$$${I}=\frac{{b}\sqrt{{a}}}{\mathrm{2}{a}}{u}+\frac{{b}\sqrt{{a}}}{\mathrm{4}{a}}{sinh}\mathrm{2}{u}+{C} \\ $$$${Since}\:{x}=\sqrt{\frac{{b}}{{a}}}{sinhu}\Rightarrow{u}={sinh}^{−\mathrm{1}} \left(\sqrt{\frac{{a}}{{b}}}{x}\right). \\ $$$${But},\:{sinh}^{−\mathrm{1}} {k}={ln}\left({k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right)\:{by}\:{definition}. \\ $$$$\therefore\:{u}={ln}\left({k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right)\:{where}\:{we}\:{let}\:{k}=\sqrt{\frac{{a}}{{b}}}{x}. \\ $$$${By}\:{definition},\:{sinh}\mathrm{2}{u}=\frac{{e}^{\mathrm{2}{u}} −{e}^{−\mathrm{2}{u}} }{\mathrm{2}}. \\ $$$${Let}\:{u}={ln}\left({g}\left({x}\right)\right)\:\Rightarrow{sinh}\mathrm{2}{u}=\frac{{e}^{\mathrm{2}{lng}\left({x}\right)} −{e}^{−\mathrm{2}{lng}\left({x}\right)} }{\mathrm{2}} \\ $$$${sinh}\mathrm{2}{u}=\frac{{g}\left({x}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{{g}\left({x}\right)^{\mathrm{2}} }}{\mathrm{2}}=\frac{{g}\left({x}\right)^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}{g}\left({x}\right)^{\mathrm{2}} }. \\ $$$${For}\:{this}\:{problem},\:{g}\left({x}\right)={k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}. \\ $$$$\Rightarrow{I}=\frac{{b}\sqrt{{a}}}{\mathrm{2}{a}}{ln}\left({k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right)+\frac{{b}\sqrt{{a}}}{\mathrm{4}{a}}\left(\frac{\left({k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}\left({k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }\right)+{C} \\ $$
Commented by Yozzii last updated on 08/Apr/16
(This post was made from my other device. Continuing solution here...) I=((b(√a))/(2a))ln((√(a/b))x+(√(((ax^2 )/b)+1)))+((b(√a))/(4a))(((((√(a/b))x+(√(((ax^2 )/b)+1)))^4 −1)/(2((√(a/b))x+(√(((ax^2 )/b)+1)))^2 )))+C I=((b(√a))/(2a))ln((√a)x+(√(ax^2 +b)))−((b(√a))/(2a))ln(√b)+((b(√(a[))(x(√a)+(√(ax^2 +b)))^4 −b^2 ])/(8ab^2 (((x(√a)+(√(ax^2 +b)))^2 )/b)))+C I=((b(√a))/(2a))ln(x(√a)+(√(ax^2 +b)))+(((x(√a)+(√(ax^2 +b)))^4 −b^2 )/(8(√a)(x(√a)+(√(ax^2 +b)))^2 ))+K K=C−((b(√a))/(2a))ln(√b)=constant of integration.
$$\left({This}\:{post}\:{was}\:{made}\:{from}\:{my}\:{other}\:{device}.\:{Continuing}\:{solution}\:{here}…\right) \\ $$$${I}=\frac{{b}\sqrt{{a}}}{\mathrm{2}{a}}{ln}\left(\sqrt{\frac{{a}}{{b}}}{x}+\sqrt{\frac{{ax}^{\mathrm{2}} }{{b}}+\mathrm{1}}\right)+\frac{{b}\sqrt{{a}}}{\mathrm{4}{a}}\left(\frac{\left(\sqrt{\frac{{a}}{{b}}}{x}+\sqrt{\frac{{ax}^{\mathrm{2}} }{{b}}+\mathrm{1}}\right)^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}\left(\sqrt{\frac{{a}}{{b}}}{x}+\sqrt{\frac{{ax}^{\mathrm{2}} }{{b}}+\mathrm{1}}\right)^{\mathrm{2}} }\right)+{C} \\ $$$${I}=\frac{{b}\sqrt{{a}}}{\mathrm{2}{a}}{ln}\left(\sqrt{{a}}{x}+\sqrt{{ax}^{\mathrm{2}} +{b}}\right)−\frac{{b}\sqrt{{a}}}{\mathrm{2}{a}}{ln}\sqrt{{b}}+\frac{\left.{b}\sqrt{{a}\left[\right.}\left({x}\sqrt{{a}}+\sqrt{{ax}^{\mathrm{2}} +{b}}\right)^{\mathrm{4}} −{b}^{\mathrm{2}} \right]}{\mathrm{8}{ab}^{\mathrm{2}} \frac{\left({x}\sqrt{{a}}+\sqrt{{ax}^{\mathrm{2}} +{b}}\right)^{\mathrm{2}} }{{b}}}+{C} \\ $$$${I}=\frac{{b}\sqrt{{a}}}{\mathrm{2}{a}}{ln}\left({x}\sqrt{{a}}+\sqrt{{ax}^{\mathrm{2}} +{b}}\right)+\frac{\left({x}\sqrt{{a}}+\sqrt{{ax}^{\mathrm{2}} +{b}}\right)^{\mathrm{4}} −{b}^{\mathrm{2}} }{\mathrm{8}\sqrt{{a}}\left({x}\sqrt{{a}}+\sqrt{{ax}^{\mathrm{2}} +{b}}\right)^{\mathrm{2}} }+{K} \\ $$$${K}={C}−\frac{{b}\sqrt{{a}}}{\mathrm{2}{a}}{ln}\sqrt{{b}}={constant}\:{of}\:{integration}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *