Menu Close

2-0-1-0-2-x-2y-8-dxdy-

Tinku Tara 0 Comments
Pin




Question Number 141431 by mohammad17 last updated on 18/May/21
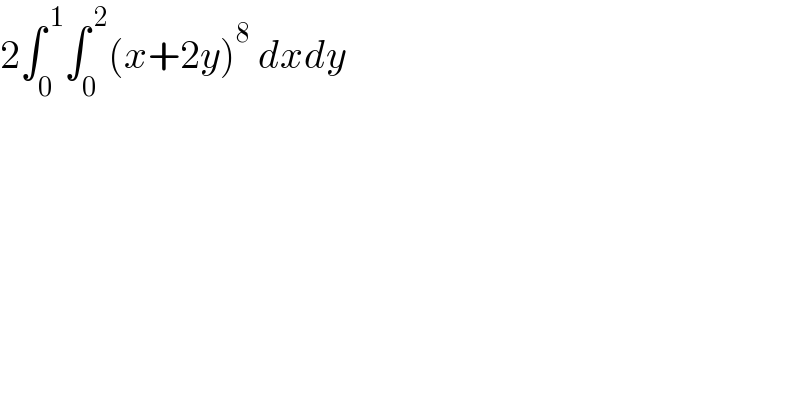
2∫_0 ^( 1) ∫_0 ^( 2) (x+2y)^8 dxdy
$$\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{2}} \left({x}+\mathrm{2}{y}\right)^{\mathrm{8}} \:{dxdy} \\ $$
Answered by mathmax by abdo last updated on 19/May/21
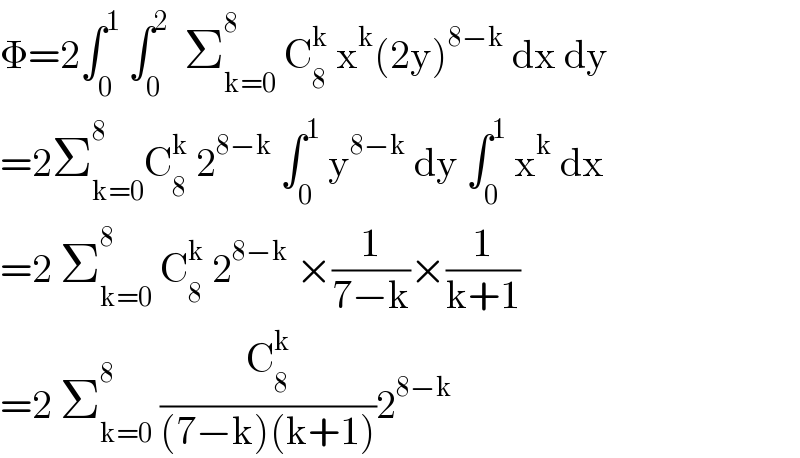
Φ=2∫_0 ^1 ∫_0 ^2 Σ_(k=0) ^8 C_8 ^k x^k (2y)^(8−k) dx dy =2Σ_(k=0) ^8 C_8 ^k 2^(8−k) ∫_0 ^1 y^(8−k) dy ∫_0 ^1 x^k dx =2 Σ_(k=0) ^8 C_8 ^k 2^(8−k) ×(1/(7−k))×(1/(k+1)) =2 Σ_(k=0) ^8 (C_8 ^k /((7−k)(k+1)))2^(8−k)
$$\Phi=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{8}} \:\mathrm{C}_{\mathrm{8}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \left(\mathrm{2y}\right)^{\mathrm{8}−\mathrm{k}} \:\mathrm{dx}\:\mathrm{dy} \\ $$$$=\mathrm{2}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{8}} \mathrm{C}_{\mathrm{8}} ^{\mathrm{k}} \:\mathrm{2}^{\mathrm{8}−\mathrm{k}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{y}^{\mathrm{8}−\mathrm{k}} \:\mathrm{dy}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{k}} \:\mathrm{dx} \\ $$$$=\mathrm{2}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{8}} \:\mathrm{C}_{\mathrm{8}} ^{\mathrm{k}} \:\mathrm{2}^{\mathrm{8}−\mathrm{k}} \:×\frac{\mathrm{1}}{\mathrm{7}−\mathrm{k}}×\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}} \\ $$$$=\mathrm{2}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{8}} \:\frac{\mathrm{C}_{\mathrm{8}} ^{\mathrm{k}} }{\left(\mathrm{7}−\mathrm{k}\right)\left(\mathrm{k}+\mathrm{1}\right)}\mathrm{2}^{\mathrm{8}−\mathrm{k}} \\ $$
Answered by mr W last updated on 19/May/21
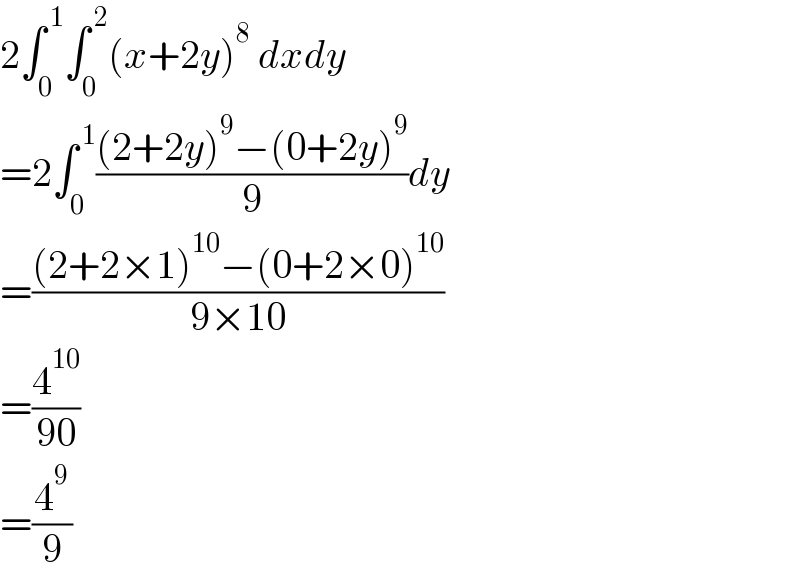
2∫_0 ^( 1) ∫_0 ^( 2) (x+2y)^8 dxdy =2∫_0 ^( 1) (((2+2y)^9 −(0+2y)^9 )/9)dy =(((2+2×1)^(10) −(0+2×0)^(10) )/(9×10)) =(4^(10) /(90)) =(4^9 /9)
$$\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{2}} \left({x}+\mathrm{2}{y}\right)^{\mathrm{8}} \:{dxdy} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{2}+\mathrm{2}{y}\right)^{\mathrm{9}} −\left(\mathrm{0}+\mathrm{2}{y}\right)^{\mathrm{9}} }{\mathrm{9}}{dy} \\ $$$$=\frac{\left(\mathrm{2}+\mathrm{2}×\mathrm{1}\right)^{\mathrm{10}} −\left(\mathrm{0}+\mathrm{2}×\mathrm{0}\right)^{\mathrm{10}} }{\mathrm{9}×\mathrm{10}} \\ $$$$=\frac{\mathrm{4}^{\mathrm{10}} }{\mathrm{90}} \\ $$$$=\frac{\mathrm{4}^{\mathrm{9}} }{\mathrm{9}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *