Question Number 9975 by Tawakalitu ayo mi last updated on 19/Jan/17

$$\int_{\:−\mathrm{2}\:} ^{\:−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{dx} \\ $$
Commented by prakash jain last updated on 20/Jan/17
![∫(1/x)dx=ln x [ln x]_(−2) ^(−1) =ln (−1)−ln (−2) ln (−1)=(2k+1)πi, k∈Z ln (−2)=ln 2+(2j+1)πi, j∈Z ln (−1)−ln (−2)=−ln 2+2nπi, n∈Z](https://www.tinkutara.com/question/Q9984.png)
$$\int\frac{\mathrm{1}}{{x}}{dx}=\mathrm{ln}\:{x} \\ $$$$\left[\mathrm{ln}\:{x}\right]_{−\mathrm{2}} ^{−\mathrm{1}} =\mathrm{ln}\:\left(−\mathrm{1}\right)−\mathrm{ln}\:\left(−\mathrm{2}\right) \\ $$$$\mathrm{ln}\:\left(−\mathrm{1}\right)=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i},\:{k}\in\mathbb{Z} \\ $$$$\mathrm{ln}\:\left(−\mathrm{2}\right)=\mathrm{ln}\:\mathrm{2}+\left(\mathrm{2}{j}+\mathrm{1}\right)\pi{i},\:{j}\in\mathbb{Z} \\ $$$$\mathrm{ln}\:\left(−\mathrm{1}\right)−\mathrm{ln}\:\left(−\mathrm{2}\right)=−\mathrm{ln}\:\mathrm{2}+\mathrm{2}{n}\pi{i},\:{n}\in\mathbb{Z} \\ $$
Commented by mrW1 last updated on 20/Jan/17
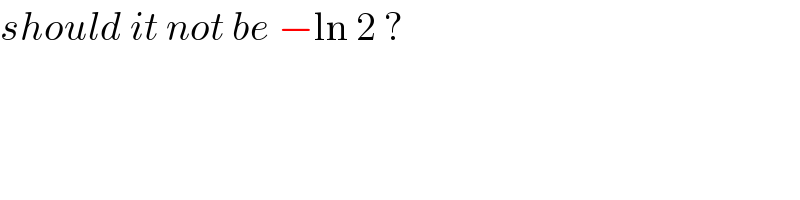
$${should}\:{it}\:{not}\:{be}\:−\mathrm{ln}\:\mathrm{2}\:? \\ $$
Commented by prakash jain last updated on 20/Jan/17
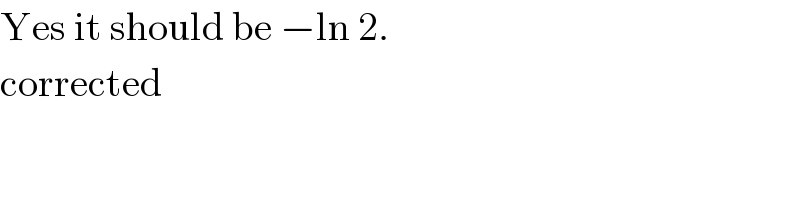
$$\mathrm{Yes}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:−\mathrm{ln}\:\mathrm{2}. \\ $$$$\mathrm{corrected} \\ $$
Commented by Tawakalitu ayo mi last updated on 20/Jan/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
