Question Number 6843 by Tawakalitu. last updated on 30/Jul/16
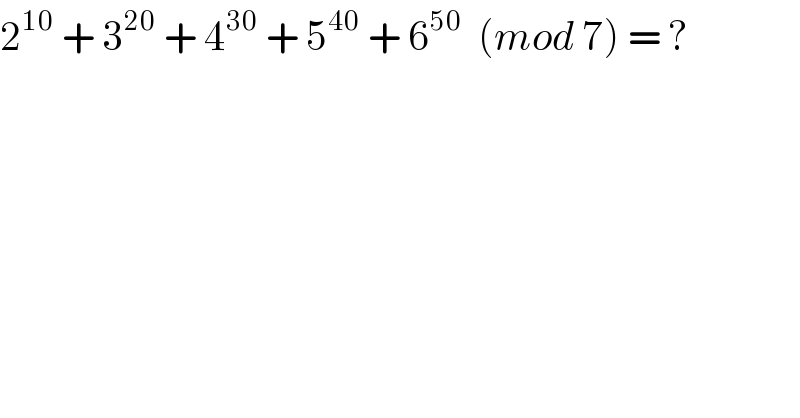
$$\mathrm{2}^{\mathrm{10}} \:+\:\mathrm{3}^{\mathrm{20}} \:+\:\mathrm{4}^{\mathrm{30}} \:+\:\mathrm{5}^{\mathrm{40}} \:+\:\mathrm{6}^{\mathrm{50}} \:\:\left({mod}\:\mathrm{7}\right)\:=\:? \\ $$
Commented by prakash jain last updated on 31/Jul/16
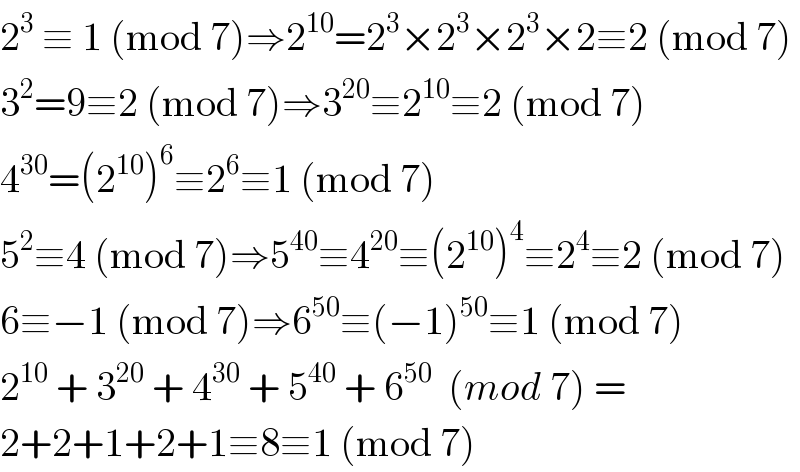
$$\mathrm{2}^{\mathrm{3}} \:\equiv\:\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{7}\right)\Rightarrow\mathrm{2}^{\mathrm{10}} =\mathrm{2}^{\mathrm{3}} ×\mathrm{2}^{\mathrm{3}} ×\mathrm{2}^{\mathrm{3}} ×\mathrm{2}\equiv\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$$$\mathrm{3}^{\mathrm{2}} =\mathrm{9}\equiv\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{7}\right)\Rightarrow\mathrm{3}^{\mathrm{20}} \equiv\mathrm{2}^{\mathrm{10}} \equiv\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$$$\mathrm{4}^{\mathrm{30}} =\left(\mathrm{2}^{\mathrm{10}} \right)^{\mathrm{6}} \equiv\mathrm{2}^{\mathrm{6}} \equiv\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$$$\mathrm{5}^{\mathrm{2}} \equiv\mathrm{4}\:\left(\mathrm{mod}\:\mathrm{7}\right)\Rightarrow\mathrm{5}^{\mathrm{40}} \equiv\mathrm{4}^{\mathrm{20}} \equiv\left(\mathrm{2}^{\mathrm{10}} \right)^{\mathrm{4}} \equiv\mathrm{2}^{\mathrm{4}} \equiv\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$$$\mathrm{6}\equiv−\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{7}\right)\Rightarrow\mathrm{6}^{\mathrm{50}} \equiv\left(−\mathrm{1}\right)^{\mathrm{50}} \equiv\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$$$\mathrm{2}^{\mathrm{10}} \:+\:\mathrm{3}^{\mathrm{20}} \:+\:\mathrm{4}^{\mathrm{30}} \:+\:\mathrm{5}^{\mathrm{40}} \:+\:\mathrm{6}^{\mathrm{50}} \:\:\left({mod}\:\mathrm{7}\right)\:=\: \\ $$$$\mathrm{2}+\mathrm{2}+\mathrm{1}+\mathrm{2}+\mathrm{1}\equiv\mathrm{8}\equiv\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$
Commented by Tawakalitu. last updated on 31/Jul/16

$${Thanks}\:{so}\:{much} \\ $$
