Question Number 72595 by zillnehu@gmail.com last updated on 30/Oct/19
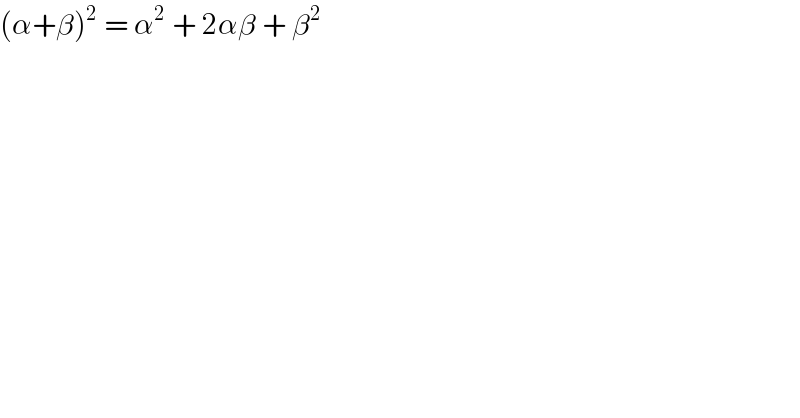
$$\left(\alpha+\beta\right)^{\mathrm{2}} \:=\:\alpha^{\mathrm{2}} \:+\:\mathrm{2}\alpha\beta\:+\:\beta^{\mathrm{2}\:} \\ $$
Commented by ajfour last updated on 30/Oct/19
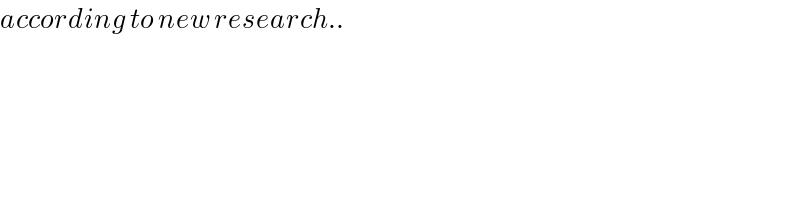
$${according}\:{to}\:{new}\:{research}.. \\ $$
Commented by MJS last updated on 30/Oct/19
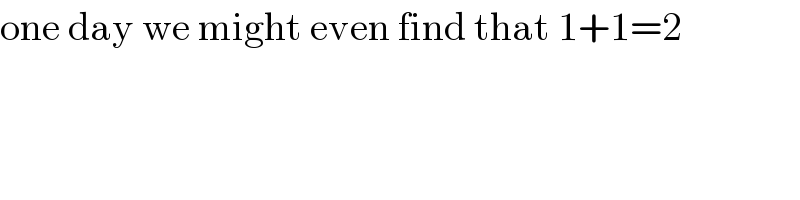
$$\mathrm{one}\:\mathrm{day}\:\mathrm{we}\:\mathrm{might}\:\mathrm{even}\:\mathrm{find}\:\mathrm{that}\:\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$
Commented by Learner-123 last updated on 30/Oct/19
if we replace, beta by -beta we may discover one more equation which will say 1-1=0 ��
Answered by Tanmay chaudhury last updated on 30/Oct/19
Commented by Tanmay chaudhury last updated on 30/Oct/19
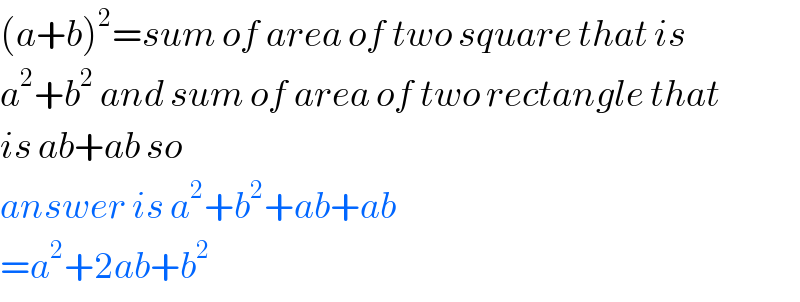
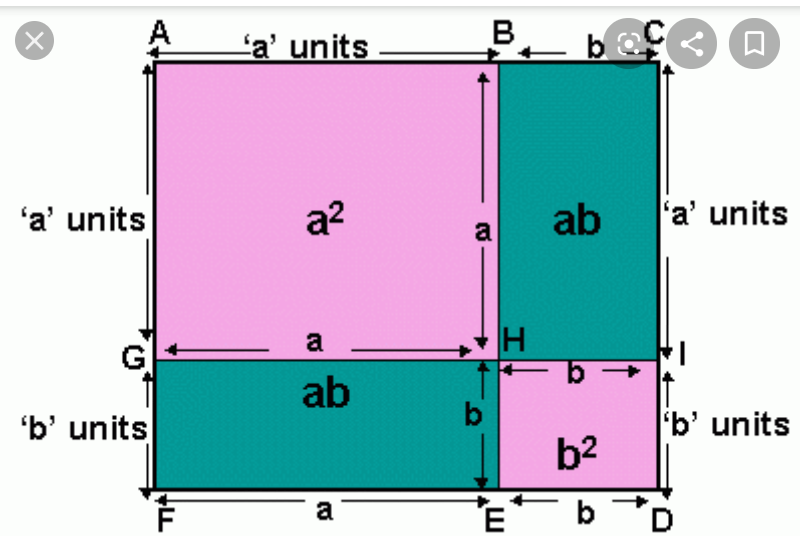
$$\left({a}+{b}\right)^{\mathrm{2}} ={sum}\:{of}\:{area}\:{of}\:{two}\:{square}\:{that}\:{is} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:{and}\:{sum}\:{of}\:{area}\:{of}\:{two}\:{rectangle}\:{that} \\ $$$${is}\:{ab}+{ab}\:{so} \\ $$$${answer}\:{is}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}+{ab} \\ $$$$={a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} \\ $$
