Question Number 8362 by Nayon last updated on 09/Oct/16
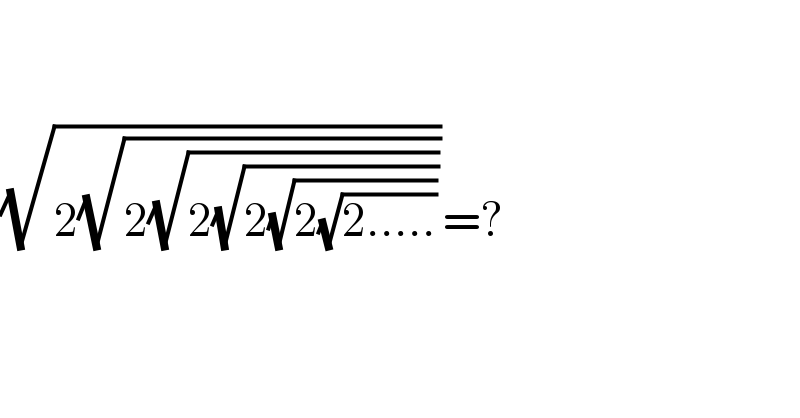
$$ \\ $$$$ \\ $$$$\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}…..}}}}}}=? \\ $$$$ \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 09/Oct/16

$$\mathrm{Let}\:\:\:\mathrm{x}=\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}…..}}}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} =\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}…..}}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} =\mathrm{2x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\left(\mathrm{x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\mathrm{0}\:\:\mid\:\:\:\mathrm{x}−\mathrm{2}=\mathrm{0}\Rightarrow\mathrm{x}=\mathrm{2} \\ $$$$\mathrm{Obviously}\:\mathrm{x}\neq\mathrm{0}\:,\mathrm{so}\:\mathrm{x}=\mathrm{2}\:\:\:\:\: \\ $$$$\:\mathrm{Hence} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}…..}}}}}}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$
