Question Number 138570 by bemath last updated on 15/Apr/21
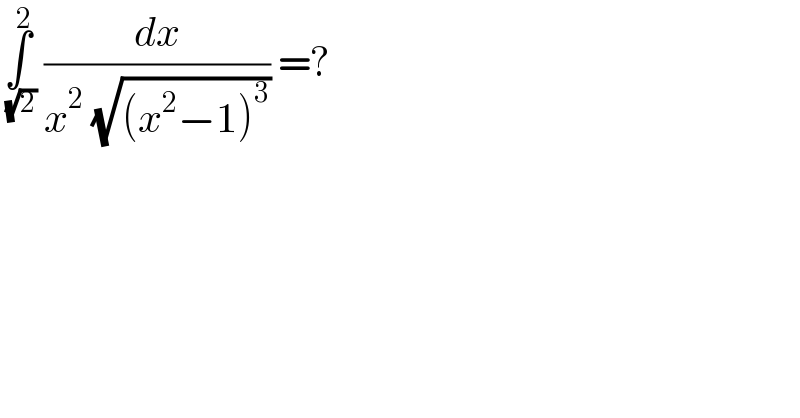
$$\underset{\:\sqrt{\mathrm{2}}} {\overset{\mathrm{2}} {\int}}\:\frac{{dx}}{{x}^{\mathrm{2}} \:\sqrt{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }}\:=?\: \\ $$
Answered by Ar Brandon last updated on 15/Apr/21
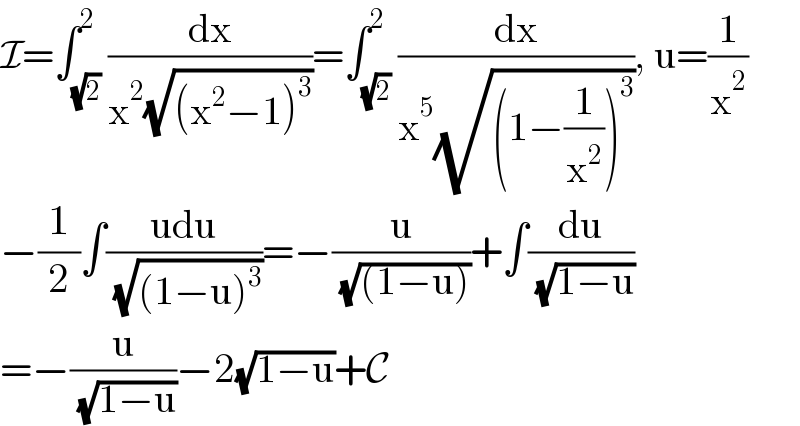
$$\mathcal{I}=\int_{\sqrt{\mathrm{2}}} ^{\mathrm{2}} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }}=\int_{\sqrt{\mathrm{2}}} ^{\mathrm{2}} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{5}} \sqrt{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{3}} }},\:\mathrm{u}=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{udu}}{\:\sqrt{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{3}} }}=−\frac{\mathrm{u}}{\:\sqrt{\left(\mathrm{1}−\mathrm{u}\right)}}+\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{1}−\mathrm{u}}} \\ $$$$=−\frac{\mathrm{u}}{\:\sqrt{\mathrm{1}−\mathrm{u}}}−\mathrm{2}\sqrt{\mathrm{1}−\mathrm{u}}+\mathcal{C} \\ $$
