Question Number 10216 by konen last updated on 30/Jan/17

$$\frac{\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{4}}+…+\sqrt{\mathrm{28}}}{\:\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}}+…+\sqrt{\mathrm{42}}}=\sqrt{\mathrm{x}}\:\Rightarrow\mathrm{x}=? \\ $$
Answered by nume1114 last updated on 30/Jan/17
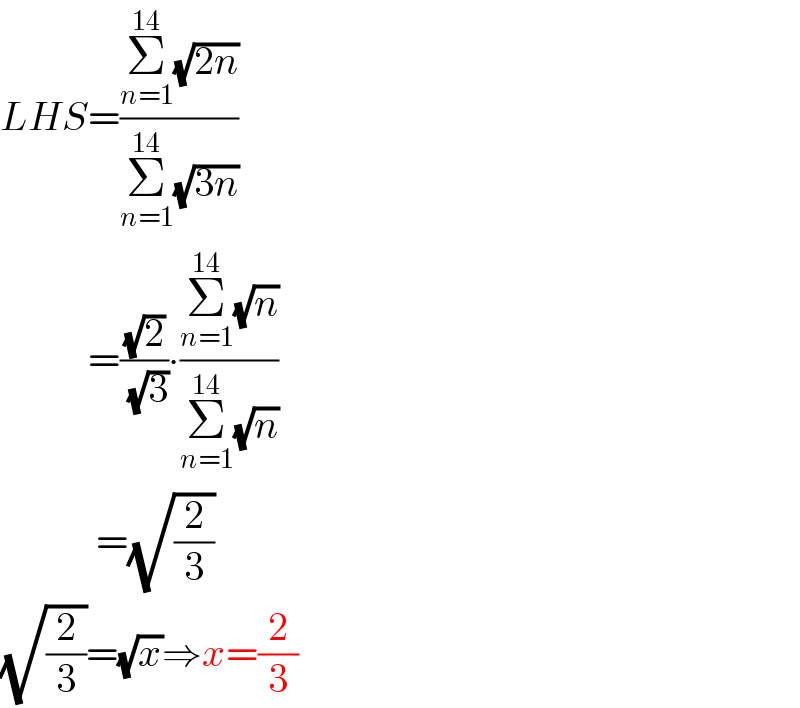
$${LHS}=\frac{\underset{{n}=\mathrm{1}} {\overset{\mathrm{14}} {\sum}}\sqrt{\mathrm{2}{n}}}{\underset{{n}=\mathrm{1}} {\overset{\mathrm{14}} {\sum}}\sqrt{\mathrm{3}{n}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\centerdot\frac{\underset{{n}=\mathrm{1}} {\overset{\mathrm{14}} {\sum}}\sqrt{{n}}}{\underset{{n}=\mathrm{1}} {\overset{\mathrm{14}} {\sum}}\sqrt{{n}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}=\sqrt{{x}}\Rightarrow{x}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by arge last updated on 04/Feb/17

$$ \\ $$$$ \\ $$$${para}\:{el}\:{numerador}, \\ $$$$ \\ $$$${a}_{\mathrm{1}} =\sqrt{\mathrm{2}} \\ $$$${a}_{{n}} =\sqrt{\mathrm{28}} \\ $$$$ \\ $$$${a}_{{n}} =\sqrt{\mathrm{2}{n}} \\ $$$${n}=\mathrm{14} \\ $$$$ \\ $$$$ \\ $$$${para}\:{el}\:{denominador}, \\ $$$$ \\ $$$${a}_{\mathrm{1}} =\sqrt{\mathrm{3}} \\ $$$${a}_{{n}} =\sqrt{\mathrm{42}} \\ $$$$ \\ $$$${a}_{{n}} =\sqrt{\mathrm{2}{n}} \\ $$$${n}=\mathrm{21} \\ $$$$ \\ $$$$\left({S}_{{n}} \right)=\frac{{n}\left({a}_{\mathrm{1}} −{a}_{{n}} \right)}{\mathrm{2}} \\ $$$$ \\ $$$$\sqrt{{x}}\:=\frac{\mathrm{7}\left(\sqrt{\:\mathrm{2}\:}\:−\sqrt{\mathrm{28}}\right)}{\frac{\mathrm{21}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\:−\sqrt{\:\mathrm{42}}\:\right)} \\ $$$$ \\ $$$${x}=\:\mathrm{0}.\mathrm{74} \\ $$$$ \\ $$
