Question Number 10429 by ridwan balatif last updated on 09/Feb/17
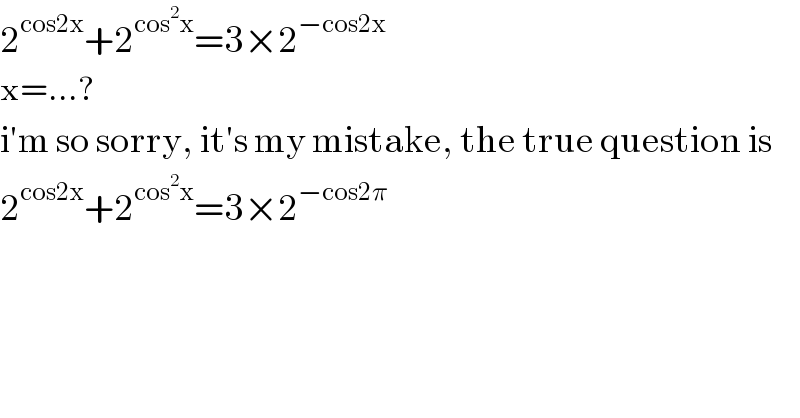
$$\mathrm{2}^{\mathrm{cos2x}} +\mathrm{2}^{\mathrm{cos}^{\mathrm{2}} \mathrm{x}} =\mathrm{3}×\mathrm{2}^{−\mathrm{cos2x}} \: \\ $$$$\mathrm{x}=…? \\ $$$$\mathrm{i}'\mathrm{m}\:\mathrm{so}\:\mathrm{sorry},\:\mathrm{it}'\mathrm{s}\:\mathrm{my}\:\mathrm{mistake},\:\mathrm{the}\:\mathrm{true}\:\mathrm{question}\:\mathrm{is} \\ $$$$\mathrm{2}^{\mathrm{cos2x}} +\mathrm{2}^{\mathrm{cos}^{\mathrm{2}} \mathrm{x}} =\mathrm{3}×\mathrm{2}^{−\mathrm{cos2}\pi} \: \\ $$
Answered by arge last updated on 09/Feb/17
![log2^(cos2x) +log2^(cos^2 x) =log(3×2^(−cos2x) ) log(2^(cos2x) 2^(cos^2 x) )=log3+log2^(−cos2x) log(2^(cos2x) 2^(cos^2 x) )−log2^(−cos2x) =log3 log[(2^(cos2x) 2^(cos^2 x) )/2^(−cos2x) ]=log3 log[(2^(cos2x) 2^(cos^2 x) )/2^(−cos2x) ]=0.48 2^(cos2x+cos^2 x+cos2x) =3 2^(cos^2 x+2cos2x) =3 cos^2 x+2cos2x=1.58 cos^2 x+2cos^2 x−2sen^2 x=1.58 3cos^2 x−2+2cos^2 x=1.58 5cos^2 x=3.58 cosx=0.85 x=32.20^°](https://www.tinkutara.com/question/Q10431.png)
$$ \\ $$$$ \\ $$$${log}\mathrm{2}^{{cos}\mathrm{2}{x}} +{log}\mathrm{2}^{{cos}^{\mathrm{2}} {x}} ={log}\left(\mathrm{3}×\mathrm{2}^{−{cos}\mathrm{2}{x}} \right) \\ $$$$ \\ $$$${log}\left(\mathrm{2}^{{cos}\mathrm{2}{x}} \mathrm{2}^{{cos}^{\mathrm{2}} {x}} \right)={log}\mathrm{3}+{log}\mathrm{2}^{−{cos}\mathrm{2}{x}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${log}\left(\mathrm{2}^{{cos}\mathrm{2}{x}} \mathrm{2}^{{cos}^{\mathrm{2}} {x}} \right)−{log}\mathrm{2}^{−{cos}\mathrm{2}{x}} ={log}\mathrm{3} \\ $$$${log}\left[\left(\mathrm{2}^{{cos}\mathrm{2}{x}} \mathrm{2}^{{cos}^{\mathrm{2}} {x}} \right)/\mathrm{2}^{−{cos}\mathrm{2}{x}} \right]={log}\mathrm{3} \\ $$$${log}\left[\left(\mathrm{2}^{{cos}\mathrm{2}{x}} \mathrm{2}^{{cos}^{\mathrm{2}} {x}} \right)/\mathrm{2}^{−{cos}\mathrm{2}{x}} \right]=\mathrm{0}.\mathrm{48} \\ $$$$\mathrm{2}^{{cos}\mathrm{2}{x}+{cos}^{\mathrm{2}} {x}+{cos}\mathrm{2}{x}} =\mathrm{3} \\ $$$$\mathrm{2}^{{cos}^{\mathrm{2}} {x}+\mathrm{2}{cos}\mathrm{2}{x}} =\mathrm{3} \\ $$$${cos}^{\mathrm{2}} {x}+\mathrm{2}{cos}\mathrm{2}{x}=\mathrm{1}.\mathrm{58} \\ $$$${cos}^{\mathrm{2}} {x}+\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{2}{sen}^{\mathrm{2}} {x}=\mathrm{1}.\mathrm{58} \\ $$$$\mathrm{3}{cos}^{\mathrm{2}} {x}−\mathrm{2}+\mathrm{2}{cos}^{\mathrm{2}} {x}=\mathrm{1}.\mathrm{58} \\ $$$$\mathrm{5}{cos}^{\mathrm{2}} {x}=\mathrm{3}.\mathrm{58} \\ $$$${cosx}=\mathrm{0}.\mathrm{85} \\ $$$${x}=\mathrm{32}.\mathrm{20}^{°} \\ $$$$ \\ $$$$ \\ $$
Commented by amir last updated on 09/Feb/17
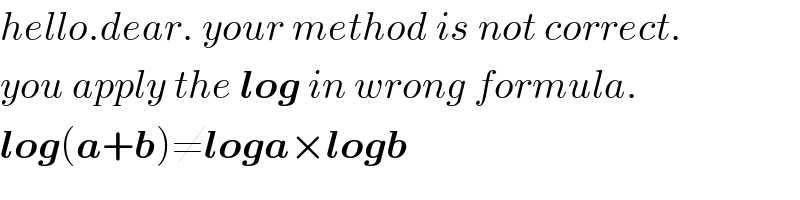
$${hello}.{dear}.\:{your}\:{method}\:{is}\:{not}\:{correct}. \\ $$$${you}\:{apply}\:{the}\:\boldsymbol{{log}}\:{in}\:{wrong}\:{formula}. \\ $$$$\boldsymbol{{log}}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)\neq\boldsymbol{{loga}}×\boldsymbol{{logb}} \\ $$
Commented by arge last updated on 10/Feb/17
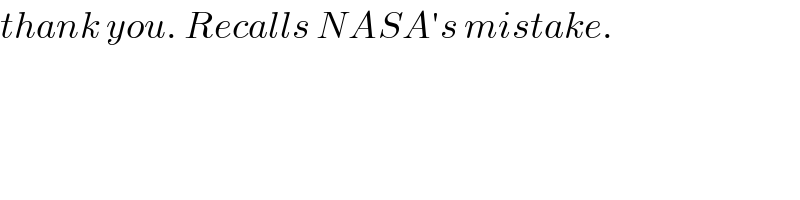
$${thank}\:{you}.\:{Recalls}\:{NASA}'{s}\:{mistake}. \\ $$
Answered by sandy_suhendra last updated on 08/Feb/17
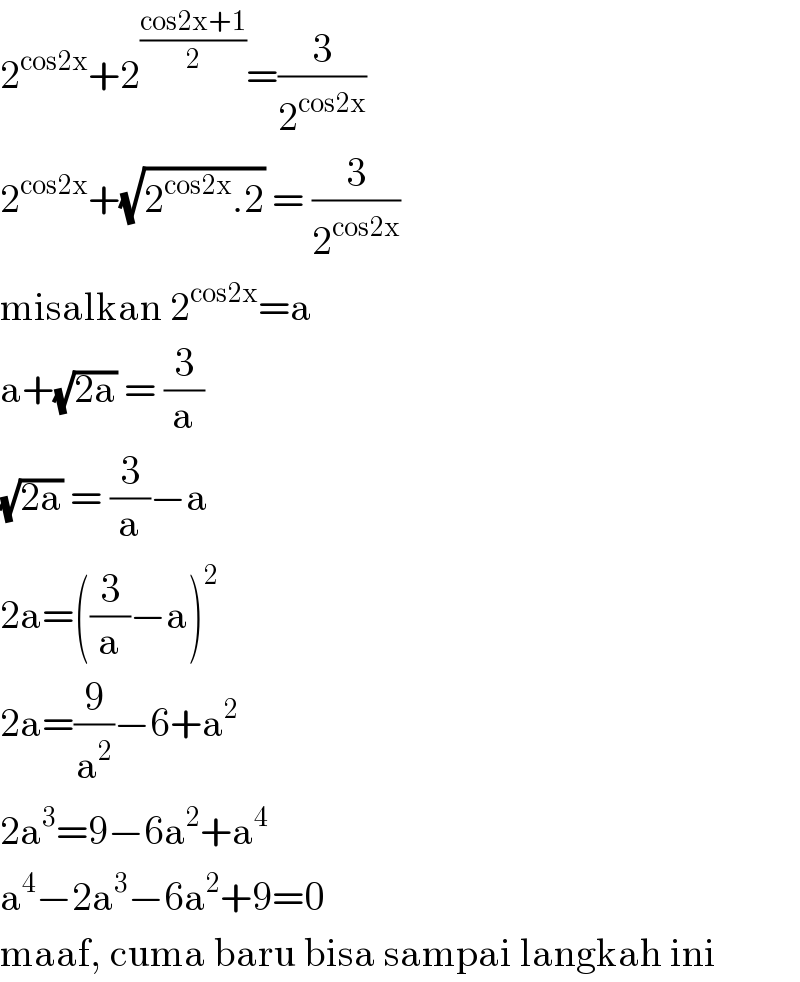
$$\mathrm{2}^{\mathrm{cos2x}} +\mathrm{2}^{\frac{\mathrm{cos2x}+\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{cos2x}} } \\ $$$$\mathrm{2}^{\mathrm{cos2x}} +\sqrt{\mathrm{2}^{\mathrm{cos2x}} .\mathrm{2}}\:=\:\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{cos2x}} } \\ $$$$\mathrm{misalkan}\:\mathrm{2}^{\mathrm{cos2x}} =\mathrm{a} \\ $$$$\mathrm{a}+\sqrt{\mathrm{2a}}\:=\:\frac{\mathrm{3}}{\mathrm{a}} \\ $$$$\sqrt{\mathrm{2a}}\:=\:\frac{\mathrm{3}}{\mathrm{a}}−\mathrm{a} \\ $$$$\mathrm{2a}=\left(\frac{\mathrm{3}}{\mathrm{a}}−\mathrm{a}\right)^{\mathrm{2}} \\ $$$$\mathrm{2a}=\frac{\mathrm{9}}{\mathrm{a}^{\mathrm{2}} }−\mathrm{6}+\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{2a}^{\mathrm{3}} =\mathrm{9}−\mathrm{6a}^{\mathrm{2}} +\mathrm{a}^{\mathrm{4}} \\ $$$$\mathrm{a}^{\mathrm{4}} −\mathrm{2a}^{\mathrm{3}} −\mathrm{6a}^{\mathrm{2}} +\mathrm{9}=\mathrm{0} \\ $$$$\mathrm{maaf},\:\mathrm{cuma}\:\mathrm{baru}\:\mathrm{bisa}\:\mathrm{sampai}\:\mathrm{langkah}\:\mathrm{ini} \\ $$
Commented by amir last updated on 09/Feb/17

Commented by amir last updated on 09/Feb/17
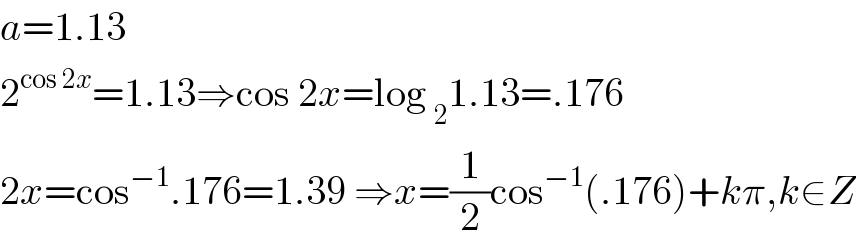
$${a}=\mathrm{1}.\mathrm{13} \\ $$$$\mathrm{2}^{\mathrm{cos}\:\mathrm{2}{x}} =\mathrm{1}.\mathrm{13}\Rightarrow\mathrm{cos}\:\mathrm{2}{x}=\mathrm{log}\:_{\mathrm{2}} \mathrm{1}.\mathrm{13}=.\mathrm{176} \\ $$$$\mathrm{2}{x}=\mathrm{cos}^{−\mathrm{1}} .\mathrm{176}=\mathrm{1}.\mathrm{39}\:\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(.\mathrm{176}\right)+{k}\pi,{k}\in{Z} \\ $$
Answered by amir last updated on 09/Feb/17
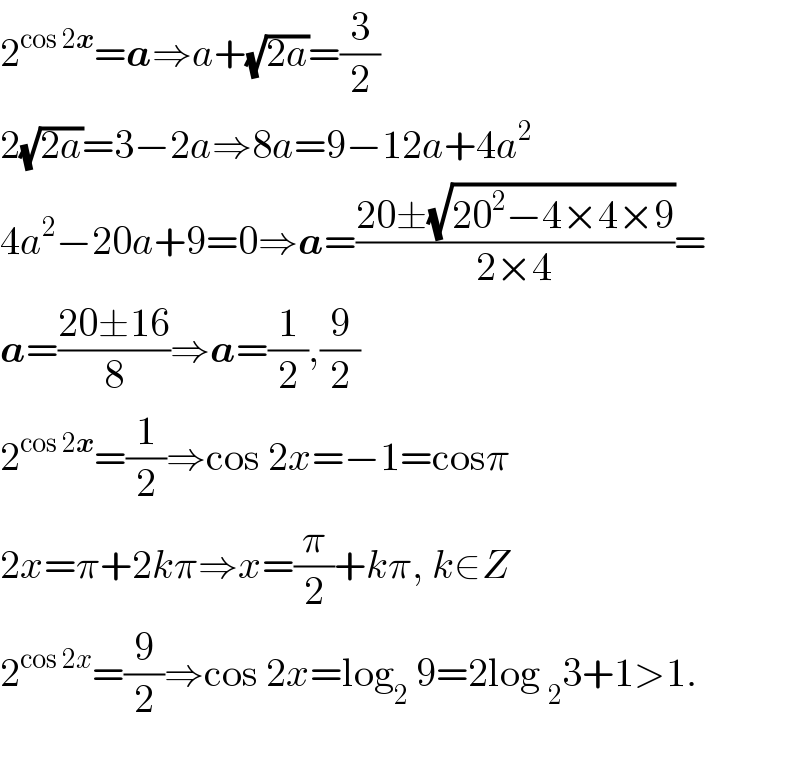
$$\mathrm{2}^{\mathrm{cos}\:\mathrm{2}\boldsymbol{{x}}} =\boldsymbol{{a}}\Rightarrow{a}+\sqrt{\mathrm{2}{a}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{2}\sqrt{\mathrm{2}{a}}=\mathrm{3}−\mathrm{2}{a}\Rightarrow\mathrm{8}{a}=\mathrm{9}−\mathrm{12}{a}+\mathrm{4}{a}^{\mathrm{2}} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −\mathrm{20}{a}+\mathrm{9}=\mathrm{0}\Rightarrow\boldsymbol{{a}}=\frac{\mathrm{20}\pm\sqrt{\mathrm{20}^{\mathrm{2}} −\mathrm{4}×\mathrm{4}×\mathrm{9}}}{\mathrm{2}×\mathrm{4}}= \\ $$$$\boldsymbol{{a}}=\frac{\mathrm{20}\pm\mathrm{16}}{\mathrm{8}}\Rightarrow\boldsymbol{{a}}=\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{cos}\:\mathrm{2}\boldsymbol{{x}}} =\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{cos}\:\mathrm{2}{x}=−\mathrm{1}=\mathrm{cos}\pi \\ $$$$\mathrm{2}{x}=\pi+\mathrm{2}{k}\pi\Rightarrow{x}=\frac{\pi}{\mathrm{2}}+{k}\pi,\:{k}\in{Z} \\ $$$$\mathrm{2}^{\mathrm{cos}\:\mathrm{2}{x}} =\frac{\mathrm{9}}{\mathrm{2}}\Rightarrow\mathrm{cos}\:\mathrm{2}{x}=\mathrm{log}_{\mathrm{2}} \:\mathrm{9}=\mathrm{2log}\:_{\mathrm{2}} \mathrm{3}+\mathrm{1}>\mathrm{1}. \\ $$$$ \\ $$
Commented by ridwan balatif last updated on 09/Feb/17

$$\mathrm{terimakasih}\:\mathrm{bantuannya},\:\mathrm{setidaknya}\:\mathrm{udah} \\ $$$$\mathrm{dapat}\:\mathrm{gambaran}\:\mathrm{penyelesaiannya} \\ $$
Commented by amir last updated on 09/Feb/17
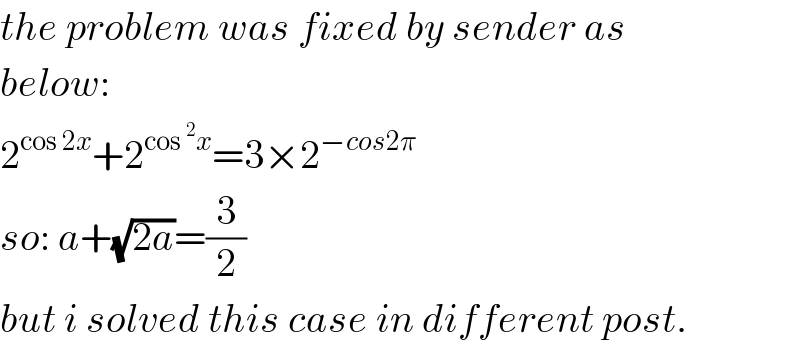
$${the}\:{problem}\:{was}\:{fixed}\:{by}\:{sender}\:{as}\: \\ $$$${below}: \\ $$$$\mathrm{2}^{\mathrm{cos}\:\mathrm{2}{x}} +\mathrm{2}^{\mathrm{cos}\:^{\mathrm{2}} {x}} =\mathrm{3}×\mathrm{2}^{−{cos}\mathrm{2}\pi} \\ $$$${so}:\:{a}+\sqrt{\mathrm{2}{a}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${but}\:{i}\:{solved}\:{this}\:{case}\:{in}\:{different}\:{post}. \\ $$
