Question Number 2770 by Yozzi last updated on 26/Nov/15
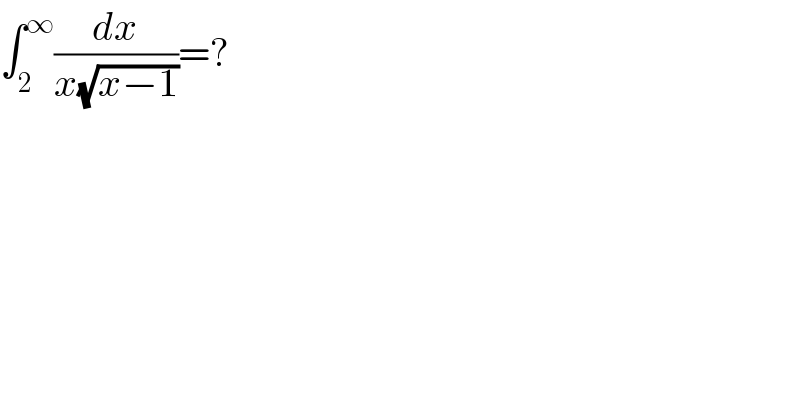
$$\int_{\mathrm{2}} ^{\infty} \frac{{dx}}{{x}\sqrt{{x}−\mathrm{1}}}=? \\ $$
Answered by prakash jain last updated on 27/Nov/15
![x−1=tan^2 u dx=2tan usec^2 udu x=sec^2 u ∫(dx/(x(√(x−1))))=∫ ((2tan usec^2 u)/(sec^2 utan u))du=∫2du=2u =2tan^(−1) ((√(x−1))) limits =2[(π/2)−(π/4)]=(π/2)](https://www.tinkutara.com/question/Q2773.png)
$${x}−\mathrm{1}=\mathrm{tan}^{\mathrm{2}} {u} \\ $$$${dx}=\mathrm{2tan}\:{u}\mathrm{sec}^{\mathrm{2}} {udu} \\ $$$${x}=\mathrm{sec}^{\mathrm{2}} {u} \\ $$$$\int\frac{{dx}}{{x}\sqrt{{x}−\mathrm{1}}}=\int\:\frac{\mathrm{2tan}\:{u}\mathrm{sec}^{\mathrm{2}} {u}}{\mathrm{sec}^{\mathrm{2}} {u}\mathrm{tan}\:{u}}{du}=\int\mathrm{2}{du}=\mathrm{2}{u} \\ $$$$=\mathrm{2tan}^{−\mathrm{1}} \left(\sqrt{{x}−\mathrm{1}}\right) \\ $$$${limits} \\ $$$$=\mathrm{2}\left[\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right]=\frac{\pi}{\mathrm{2}} \\ $$
