Question Number 8807 by tawakalitu last updated on 28/Oct/16
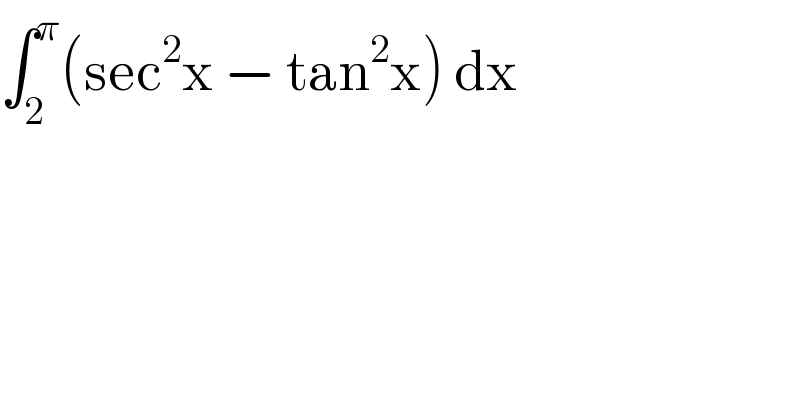
$$\int_{\mathrm{2}} ^{\pi} \left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}\:−\:\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{dx} \\ $$
Answered by ridwan balatif last updated on 29/Oct/16
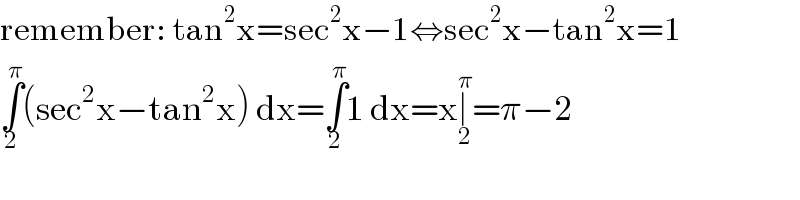
$$\mathrm{remember}:\:\mathrm{tan}^{\mathrm{2}} \mathrm{x}=\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\Leftrightarrow\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}=\mathrm{1} \\ $$$$\underset{\mathrm{2}} {\overset{\pi} {\int}}\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{dx}=\underset{\mathrm{2}} {\overset{\pi} {\int}}\mathrm{1}\:\mathrm{dx}=\mathrm{x}\underset{\mathrm{2}} {\overset{\pi} {\mid}}=\pi−\mathrm{2} \\ $$
Commented by tawakalitu last updated on 29/Oct/16
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
