Menu Close

2-x-1-2-4-y-2-2-5-z-2-9-4-4-x-1-2-2-x-2-2-1-z-2-1-2-3-z-1-2-6-y-2-2-2-z-2-1-z-1-2-y-2-2-z-2-

Tinku Tara 0 Comments
Pin




Question Number 11074 by Joel576 last updated on 10/Mar/17
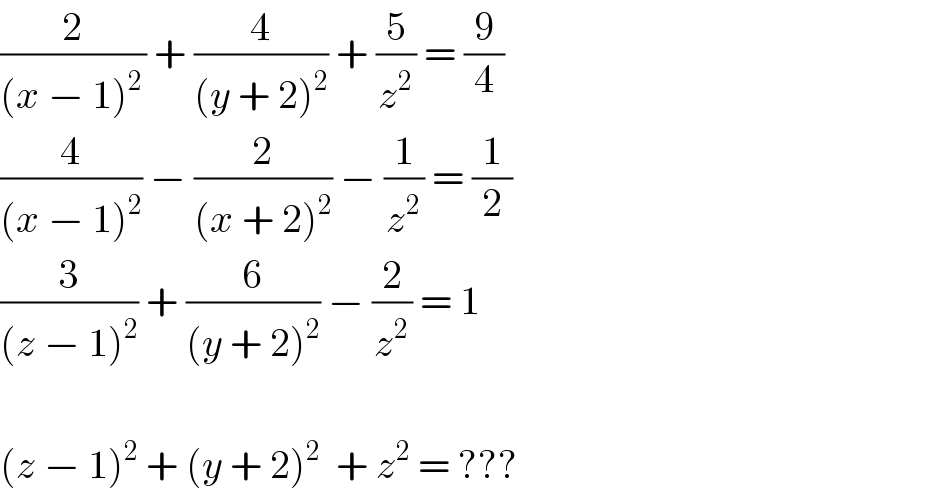
(2/((x − 1)^(2 ) )) + (4/((y + 2)^2 )) + (5/z^2 ) = (9/4) (4/((x − 1)^2 )) − (2/((x + 2)^2 )) − (1/z^2 ) = (1/2) (3/((z − 1)^2 )) + (6/((y + 2)^2 )) − (2/z^2 ) = 1 (z − 1)^2 + (y + 2)^2 + z^2 = ???
$$\frac{\mathrm{2}}{\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}\:} }\:+\:\frac{\mathrm{4}}{\left({y}\:+\:\mathrm{2}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{5}}{{z}^{\mathrm{2}} }\:=\:\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\frac{\mathrm{4}}{\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} }\:−\:\frac{\mathrm{2}}{\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{{z}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{3}}{\left({z}\:−\:\mathrm{1}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{6}}{\left({y}\:+\:\mathrm{2}\right)^{\mathrm{2}} }\:−\:\frac{\mathrm{2}}{{z}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$ \\ $$$$\left({z}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:+\:\left({y}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:\:+\:{z}^{\mathrm{2}} \:=\:??? \\ $$
Answered by ridwan balatif last updated on 10/Mar/17
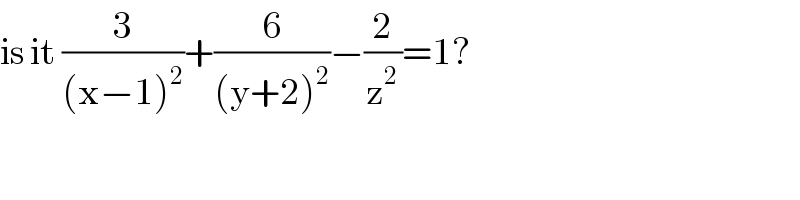
is it (3/((x−1)^2 ))+(6/((y+2)^2 ))−(2/z^2 )=1?
$$\mathrm{is}\:\mathrm{it}\:\frac{\mathrm{3}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{6}}{\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{z}^{\mathrm{2}} }=\mathrm{1}? \\ $$
Commented by Joel576 last updated on 11/Mar/17
Commented by Joel576 last updated on 11/Mar/17
tapi bisa juga soalnya typo
$$\mathrm{tapi}\:\mathrm{bisa}\:\mathrm{juga}\:\mathrm{soalnya}\:\mathrm{typo} \\ $$
Commented by ridwan balatif last updated on 11/Mar/17
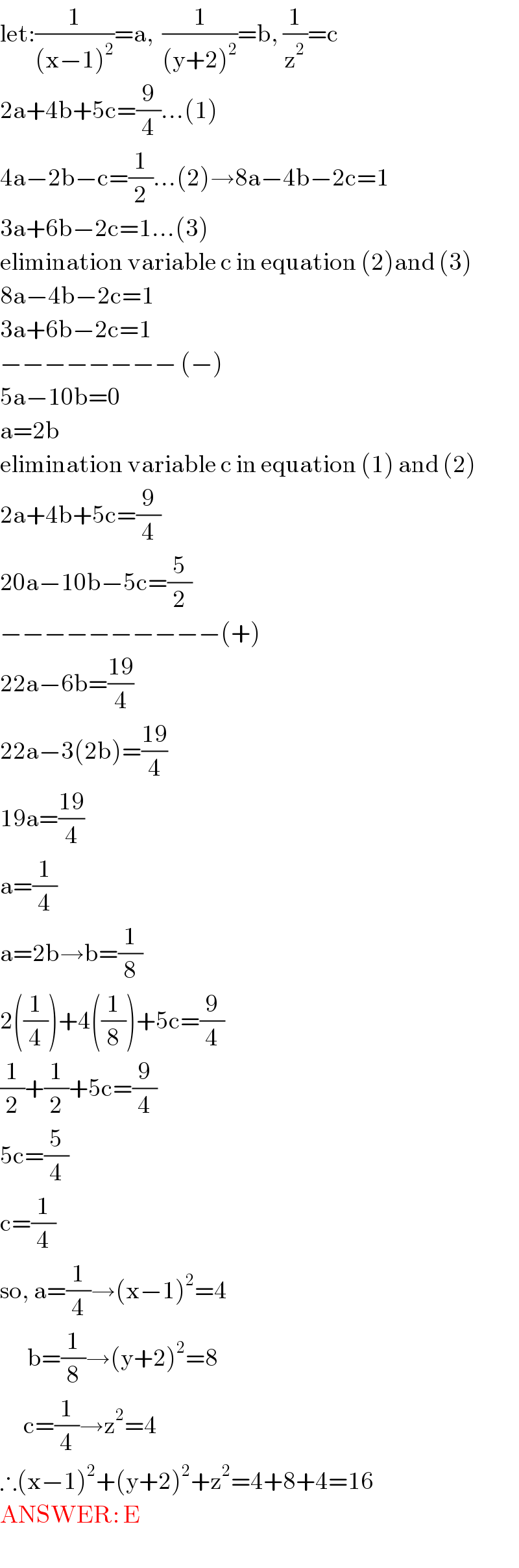
let:(1/((x−1)^2 ))=a, (1/((y+2)^2 ))=b, (1/z^2 )=c 2a+4b+5c=(9/4)...(1) 4a−2b−c=(1/2)...(2)→8a−4b−2c=1 3a+6b−2c=1...(3) elimination variable c in equation (2)and (3) 8a−4b−2c=1 3a+6b−2c=1 −−−−−−−− (−) 5a−10b=0 a=2b elimination variable c in equation (1) and (2) 2a+4b+5c=(9/4) 20a−10b−5c=(5/2) −−−−−−−−−−(+) 22a−6b=((19)/4) 22a−3(2b)=((19)/4) 19a=((19)/4) a=(1/4) a=2b→b=(1/8) 2((1/4))+4((1/8))+5c=(9/4) (1/2)+(1/2)+5c=(9/4) 5c=(5/4) c=(1/4) so, a=(1/4)→(x−1)^2 =4 b=(1/8)→(y+2)^2 =8 c=(1/4)→z^2 =4 ∴(x−1)^2 +(y+2)^2 +z^2 =4+8+4=16 ANSWER: E
$$\mathrm{let}:\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{a},\:\:\frac{\mathrm{1}}{\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{b},\:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }=\mathrm{c} \\ $$$$\mathrm{2a}+\mathrm{4b}+\mathrm{5c}=\frac{\mathrm{9}}{\mathrm{4}}…\left(\mathrm{1}\right) \\ $$$$\mathrm{4a}−\mathrm{2b}−\mathrm{c}=\frac{\mathrm{1}}{\mathrm{2}}…\left(\mathrm{2}\right)\rightarrow\mathrm{8a}−\mathrm{4b}−\mathrm{2c}=\mathrm{1} \\ $$$$\mathrm{3a}+\mathrm{6b}−\mathrm{2c}=\mathrm{1}…\left(\mathrm{3}\right) \\ $$$$\mathrm{elimination}\:\mathrm{variable}\:\mathrm{c}\:\mathrm{in}\:\mathrm{equation}\:\left(\mathrm{2}\right)\mathrm{and}\:\left(\mathrm{3}\right) \\ $$$$\mathrm{8a}−\mathrm{4b}−\mathrm{2c}=\mathrm{1} \\ $$$$\mathrm{3a}+\mathrm{6b}−\mathrm{2c}=\mathrm{1} \\ $$$$−−−−−−−−\:\left(−\right) \\ $$$$\mathrm{5a}−\mathrm{10b}=\mathrm{0} \\ $$$$\mathrm{a}=\mathrm{2b} \\ $$$$\mathrm{elimination}\:\mathrm{variable}\:\mathrm{c}\:\mathrm{in}\:\mathrm{equation}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{2a}+\mathrm{4b}+\mathrm{5c}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{20a}−\mathrm{10b}−\mathrm{5c}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$−−−−−−−−−−\left(+\right) \\ $$$$\mathrm{22a}−\mathrm{6b}=\frac{\mathrm{19}}{\mathrm{4}} \\ $$$$\mathrm{22a}−\mathrm{3}\left(\mathrm{2b}\right)=\frac{\mathrm{19}}{\mathrm{4}} \\ $$$$\mathrm{19a}=\frac{\mathrm{19}}{\mathrm{4}} \\ $$$$\mathrm{a}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{a}=\mathrm{2b}\rightarrow\mathrm{b}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{8}}\right)+\mathrm{5c}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{5c}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{5c}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\mathrm{c}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{so},\:\mathrm{a}=\frac{\mathrm{1}}{\mathrm{4}}\rightarrow\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\mathrm{b}=\frac{\mathrm{1}}{\mathrm{8}}\rightarrow\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{8} \\ $$$$\:\:\:\:\:\:\mathrm{c}=\frac{\mathrm{1}}{\mathrm{4}}\rightarrow\mathrm{z}^{\mathrm{2}} =\mathrm{4} \\ $$$$\therefore\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} =\mathrm{4}+\mathrm{8}+\mathrm{4}=\mathrm{16} \\ $$$$\mathrm{ANSWER}:\:\mathrm{E} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *