Menu Close

2-x-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 136907 by leena12345 last updated on 27/Mar/21
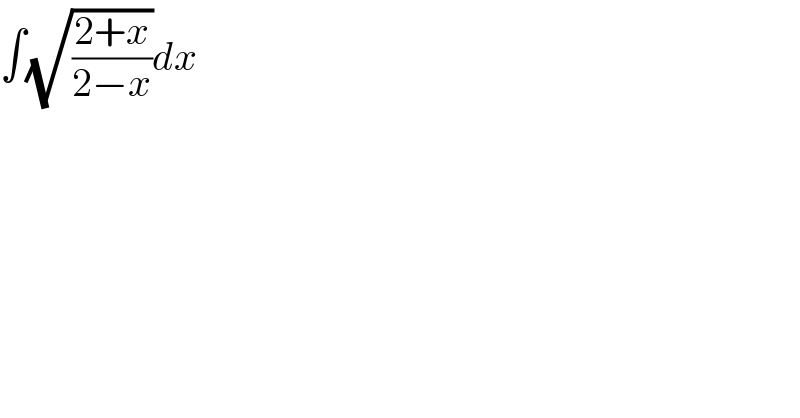
∫(√((2+x)/(2−x)))dx
$$\int\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}{dx} \\ $$
Answered by Mathspace last updated on 27/Mar/21
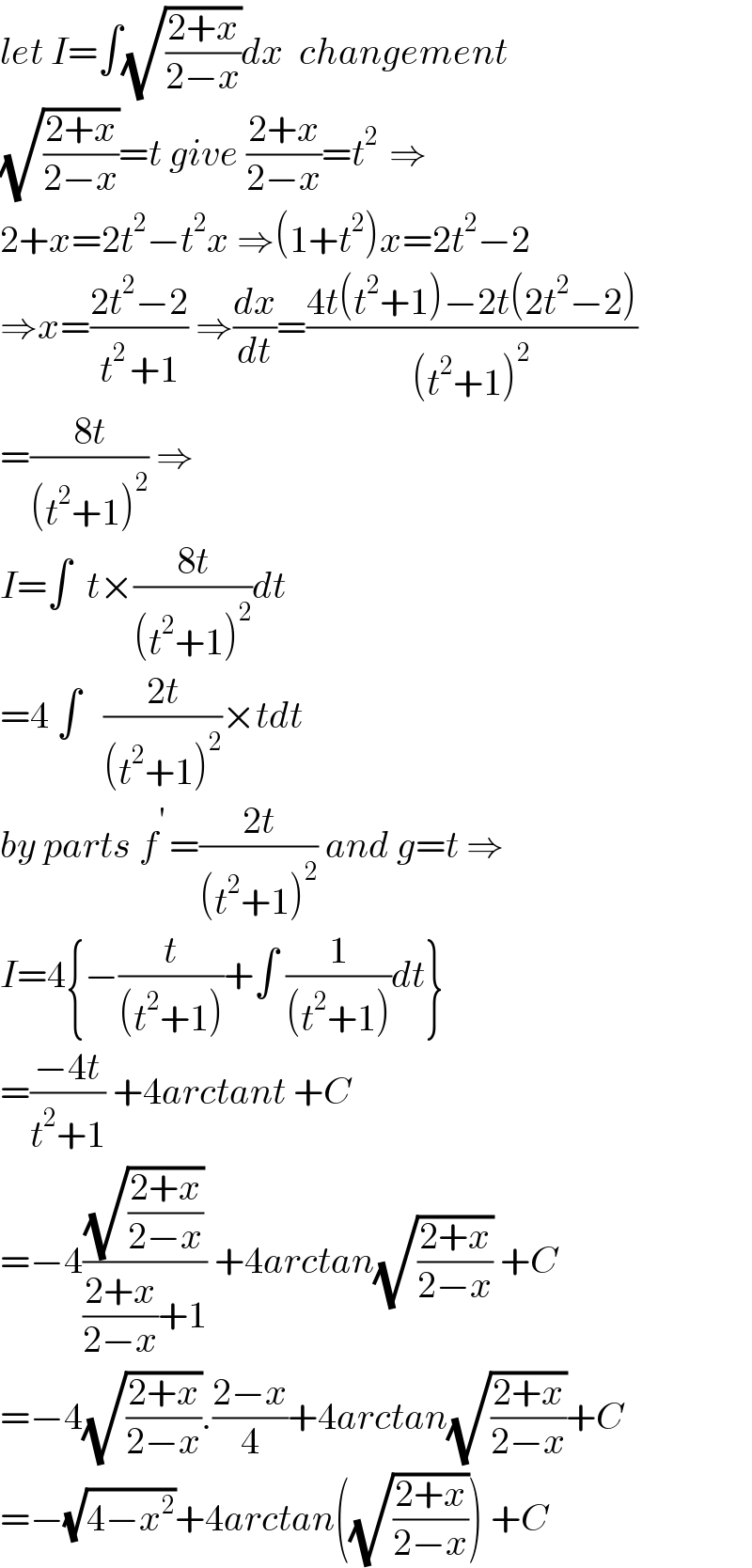
let I=∫(√((2+x)/(2−x)))dx changement (√((2+x)/(2−x)))=t give ((2+x)/(2−x))=t^(2 ) ⇒ 2+x=2t^2 −t^2 x ⇒(1+t^2 )x=2t^2 −2 ⇒x=((2t^2 −2)/(t^(2 ) +1)) ⇒(dx/dt)=((4t(t^2 +1)−2t(2t^2 −2))/((t^2 +1)^2 )) =((8t)/((t^2 +1)^2 )) ⇒ I=∫ t×((8t)/((t^2 +1)^2 ))dt =4 ∫ ((2t)/((t^2 +1)^2 ))×tdt by parts f^(′ ) =((2t)/((t^2 +1)^2 )) and g=t ⇒ I=4{−(t/((t^2 +1)))+∫ (1/((t^2 +1)))dt} =((−4t)/(t^2 +1)) +4arctant +C =−4((√((2+x)/(2−x)))/(((2+x)/(2−x))+1)) +4arctan(√((2+x)/(2−x))) +C =−4(√((2+x)/(2−x))).((2−x)/4)+4arctan(√((2+x)/(2−x)))+C =−(√(4−x^2 ))+4arctan((√((2+x)/(2−x)))) +C
$${let}\:{I}=\int\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}{dx}\:\:{changement} \\ $$$$\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}={t}\:{give}\:\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}={t}^{\mathrm{2}\:} \:\Rightarrow \\ $$$$\mathrm{2}+{x}=\mathrm{2}{t}^{\mathrm{2}} −{t}^{\mathrm{2}} {x}\:\Rightarrow\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}=\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}}{{t}^{\mathrm{2}\:} +\mathrm{1}}\:\Rightarrow\frac{{dx}}{{dt}}=\frac{\mathrm{4}{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2}{t}\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{8}{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}=\int\:\:{t}×\frac{\mathrm{8}{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{4}\:\int\:\:\:\frac{\mathrm{2}{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }×{tdt} \\ $$$${by}\:{parts}\:{f}^{'\:} =\frac{\mathrm{2}{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{and}\:{g}={t}\:\Rightarrow \\ $$$${I}=\mathrm{4}\left\{−\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)}+\int\:\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{dt}\right\} \\ $$$$=\frac{−\mathrm{4}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\:+\mathrm{4}{arctant}\:+{C} \\ $$$$=−\mathrm{4}\frac{\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}}{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}+\mathrm{1}}\:+\mathrm{4}{arctan}\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}\:+{C} \\ $$$$=−\mathrm{4}\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}.\frac{\mathrm{2}−{x}}{\mathrm{4}}+\mathrm{4}{arctan}\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}+{C} \\ $$$$=−\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }+\mathrm{4}{arctan}\left(\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}\right)\:+{C} \\ $$
Answered by Dwaipayan Shikari last updated on 27/Mar/21
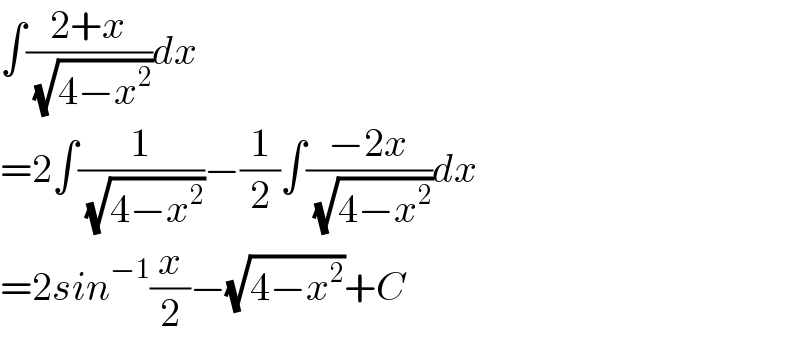
∫((2+x)/( (√(4−x^2 ))))dx =2∫(1/( (√(4−x^2 ))))−(1/2)∫((−2x)/( (√(4−x^2 ))))dx =2sin^(−1) (x/2)−(√(4−x^2 ))+C
$$\int\frac{\mathrm{2}+{x}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\mathrm{2}\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−\mathrm{2}{x}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\mathrm{2}{sin}^{−\mathrm{1}} \frac{{x}}{\mathrm{2}}−\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }+{C} \\ $$
Answered by Mathspace last updated on 27/Mar/21
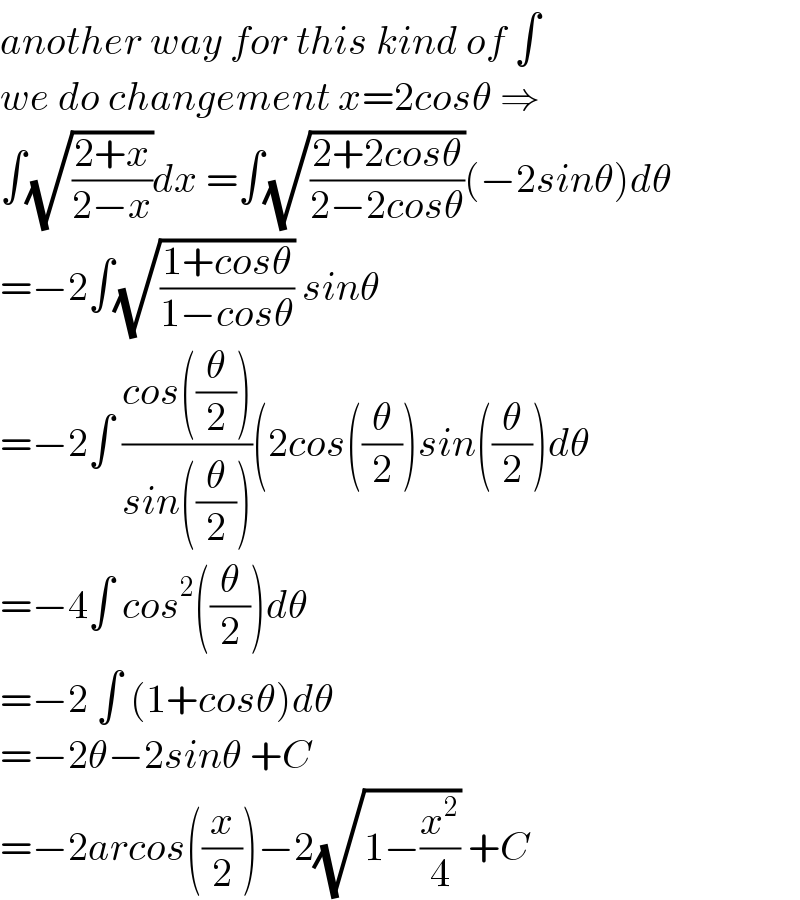
another way for this kind of ∫ we do changement x=2cosθ ⇒ ∫(√((2+x)/(2−x)))dx =∫(√((2+2cosθ)/(2−2cosθ)))(−2sinθ)dθ =−2∫(√((1+cosθ)/(1−cosθ))) sinθ =−2∫ ((cos((θ/2)))/(sin((θ/2))))(2cos((θ/2))sin((θ/2))dθ =−4∫ cos^2 ((θ/2))dθ =−2 ∫ (1+cosθ)dθ =−2θ−2sinθ +C =−2arcos((x/2))−2(√(1−(x^2 /4))) +C
$${another}\:{way}\:{for}\:{this}\:{kind}\:{of}\:\int \\ $$$${we}\:{do}\:{changement}\:{x}=\mathrm{2}{cos}\theta\:\Rightarrow \\ $$$$\int\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}{dx}\:=\int\sqrt{\frac{\mathrm{2}+\mathrm{2}{cos}\theta}{\mathrm{2}−\mathrm{2}{cos}\theta}}\left(−\mathrm{2}{sin}\theta\right){d}\theta \\ $$$$=−\mathrm{2}\int\sqrt{\frac{\mathrm{1}+{cos}\theta}{\mathrm{1}−{cos}\theta}}\:{sin}\theta \\ $$$$=−\mathrm{2}\int\:\frac{{cos}\left(\frac{\theta}{\mathrm{2}}\right)}{{sin}\left(\frac{\theta}{\mathrm{2}}\right)}\left(\mathrm{2}{cos}\left(\frac{\theta}{\mathrm{2}}\right){sin}\left(\frac{\theta}{\mathrm{2}}\right){d}\theta\right. \\ $$$$=−\mathrm{4}\int\:{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right){d}\theta \\ $$$$=−\mathrm{2}\:\int\:\left(\mathrm{1}+{cos}\theta\right){d}\theta \\ $$$$=−\mathrm{2}\theta−\mathrm{2}{sin}\theta\:+{C} \\ $$$$=−\mathrm{2}{arcos}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{2}\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\:+{C} \\ $$
Answered by liberty last updated on 27/Mar/21
I=∫ (√((2+x)/(2−x))) dx let x = 2cos 2α ⇒dx=−4sin 2α dα I=−4∫sin 2α (√((2+2cos 2α)/(2−2cos 2α))) dα I=−4∫ sin 2α (√((2(2sin^2 α))/(2(2cos^2 α)))) dα I=−4∫ sin 2α (((sin α)/(cos α))) dα I=−8∫ sin^2 α dα I=∫ (−4+4cos 2α)dα I=−4α+2sin 2α + c I=−4 (((arccos ((x/2)))/2))+2(√(1−(x^2 /4))) + c I=−2arccos ((x/2))+(√(4−x^2 )) + c
$$\mathrm{I}=\int\:\sqrt{\frac{\mathrm{2}+\mathrm{x}}{\mathrm{2}−\mathrm{x}}}\:\mathrm{dx}\: \\ $$$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{2cos}\:\mathrm{2}\alpha\:\Rightarrow\mathrm{dx}=−\mathrm{4sin}\:\mathrm{2}\alpha\:\mathrm{d}\alpha \\ $$$$\mathrm{I}=−\mathrm{4}\int\mathrm{sin}\:\mathrm{2}\alpha\:\sqrt{\frac{\mathrm{2}+\mathrm{2cos}\:\mathrm{2}\alpha}{\mathrm{2}−\mathrm{2cos}\:\mathrm{2}\alpha}}\:\mathrm{d}\alpha \\ $$$$\mathrm{I}=−\mathrm{4}\int\:\mathrm{sin}\:\mathrm{2}\alpha\:\sqrt{\frac{\mathrm{2}\left(\mathrm{2sin}\:^{\mathrm{2}} \alpha\right)}{\mathrm{2}\left(\mathrm{2cos}\:^{\mathrm{2}} \alpha\right)}}\:\mathrm{d}\alpha \\ $$$$\mathrm{I}=−\mathrm{4}\int\:\mathrm{sin}\:\mathrm{2}\alpha\:\left(\frac{\mathrm{sin}\:\alpha}{\mathrm{cos}\:\alpha}\right)\:\mathrm{d}\alpha \\ $$$$\mathrm{I}=−\mathrm{8}\int\:\mathrm{sin}\:^{\mathrm{2}} \alpha\:\mathrm{d}\alpha \\ $$$$\mathrm{I}=\int\:\left(−\mathrm{4}+\mathrm{4cos}\:\mathrm{2}\alpha\right)\mathrm{d}\alpha \\ $$$$\mathrm{I}=−\mathrm{4}\alpha+\mathrm{2sin}\:\mathrm{2}\alpha\:+\:\mathrm{c} \\ $$$$\mathrm{I}=−\mathrm{4}\:\left(\frac{\mathrm{arccos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{2}}\right)+\mathrm{2}\sqrt{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}}\:+\:\mathrm{c} \\ $$$$\mathrm{I}=−\mathrm{2arccos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\:+\:\mathrm{c}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *