Question Number 5476 by love math last updated on 15/May/16

$$\int\frac{\mathrm{2}^{{x}} \mathrm{3}^{{x}} }{\mathrm{9}^{{x}} −\mathrm{4}^{{x}} }{dx} \\ $$$$ \\ $$$$\int\frac{{dx}}{\left(\mathrm{1}+{x}\right)\sqrt{{x}}} \\ $$
Answered by Yozzii last updated on 15/May/16
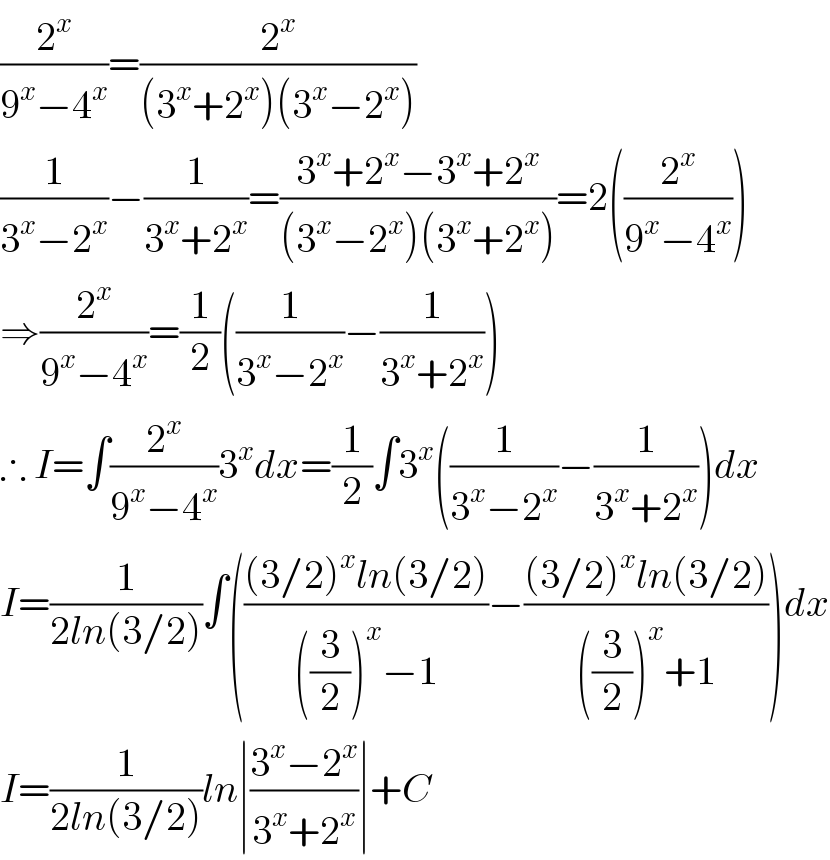
$$\frac{\mathrm{2}^{{x}} }{\mathrm{9}^{{x}} −\mathrm{4}^{{x}} }=\frac{\mathrm{2}^{{x}} }{\left(\mathrm{3}^{{x}} +\mathrm{2}^{{x}} \right)\left(\mathrm{3}^{{x}} −\mathrm{2}^{{x}} \right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}^{{x}} −\mathrm{2}^{{x}} }−\frac{\mathrm{1}}{\mathrm{3}^{{x}} +\mathrm{2}^{{x}} }=\frac{\mathrm{3}^{{x}} +\mathrm{2}^{{x}} −\mathrm{3}^{{x}} +\mathrm{2}^{{x}} }{\left(\mathrm{3}^{{x}} −\mathrm{2}^{{x}} \right)\left(\mathrm{3}^{{x}} +\mathrm{2}^{{x}} \right)}=\mathrm{2}\left(\frac{\mathrm{2}^{{x}} }{\mathrm{9}^{{x}} −\mathrm{4}^{{x}} }\right) \\ $$$$\Rightarrow\frac{\mathrm{2}^{{x}} }{\mathrm{9}^{{x}} −\mathrm{4}^{{x}} }=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}^{{x}} −\mathrm{2}^{{x}} }−\frac{\mathrm{1}}{\mathrm{3}^{{x}} +\mathrm{2}^{{x}} }\right) \\ $$$$\therefore\:{I}=\int\frac{\mathrm{2}^{{x}} }{\mathrm{9}^{{x}} −\mathrm{4}^{{x}} }\mathrm{3}^{{x}} {dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{3}^{{x}} \left(\frac{\mathrm{1}}{\mathrm{3}^{{x}} −\mathrm{2}^{{x}} }−\frac{\mathrm{1}}{\mathrm{3}^{{x}} +\mathrm{2}^{{x}} }\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{3}/\mathrm{2}\right)}\int\left(\frac{\left(\mathrm{3}/\mathrm{2}\right)^{{x}} {ln}\left(\mathrm{3}/\mathrm{2}\right)}{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{x}} −\mathrm{1}}−\frac{\left(\mathrm{3}/\mathrm{2}\right)^{{x}} {ln}\left(\mathrm{3}/\mathrm{2}\right)}{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{x}} +\mathrm{1}}\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{3}/\mathrm{2}\right)}{ln}\mid\frac{\mathrm{3}^{{x}} −\mathrm{2}^{{x}} }{\mathrm{3}^{{x}} +\mathrm{2}^{{x}} }\mid+{C} \\ $$
Commented by Yozzii last updated on 15/May/16

$${Let}\:{j}={a}^{{x}} \:\:\:{a}>\mathrm{0} \\ $$$$\Rightarrow{lnj}={xlna} \\ $$$${By}\:{implicit}\:{differentiation} \\ $$$$\Rightarrow{j}^{−\mathrm{1}} {j}'={lna}\Rightarrow\frac{{dj}}{{dx}}={jlna}={a}^{{x}} {lna} \\ $$$$\Rightarrow\int\frac{{a}^{{x}} {lna}}{{qa}^{{x}} +{b}}{dx}=\int\frac{\mathrm{1}}{{qu}+{b}}{du}=\frac{\mathrm{1}}{{q}}{ln}\mid{qu}+{b}\mid+{C}=\frac{\mathrm{1}}{{q}}{ln}\mid{qa}^{{x}} +{b}\mid+{C}\:{where}\:{u}={a}^{{x}} . \\ $$
Answered by Yozzii last updated on 15/May/16
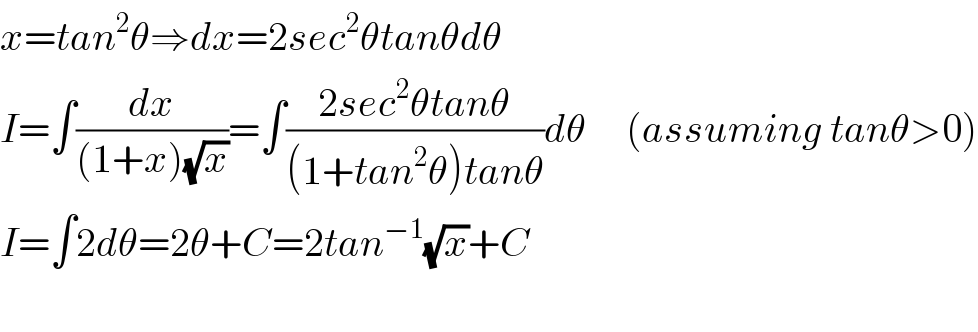
$${x}={tan}^{\mathrm{2}} \theta\Rightarrow{dx}=\mathrm{2}{sec}^{\mathrm{2}} \theta{tan}\theta{d}\theta \\ $$$${I}=\int\frac{{dx}}{\left(\mathrm{1}+{x}\right)\sqrt{{x}}}=\int\frac{\mathrm{2}{sec}^{\mathrm{2}} \theta{tan}\theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){tan}\theta}{d}\theta\:\:\:\:\:\left({assuming}\:{tan}\theta>\mathrm{0}\right) \\ $$$${I}=\int\mathrm{2}{d}\theta=\mathrm{2}\theta+{C}=\mathrm{2}{tan}^{−\mathrm{1}} \sqrt{{x}}+{C}\: \\ $$$$ \\ $$
