Question Number 77221 by john santu last updated on 04/Jan/20
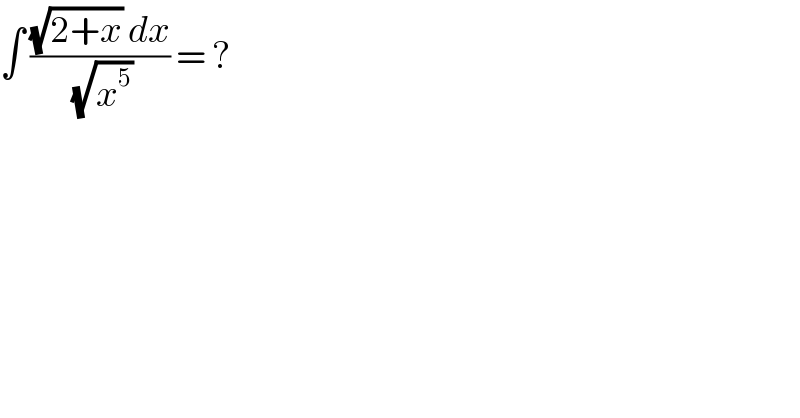
$$\int\:\frac{\sqrt{\mathrm{2}+{x}}\:{dx}}{\:\sqrt{{x}^{\mathrm{5}} }}\:=\:? \\ $$
Answered by jagoll last updated on 04/Jan/20
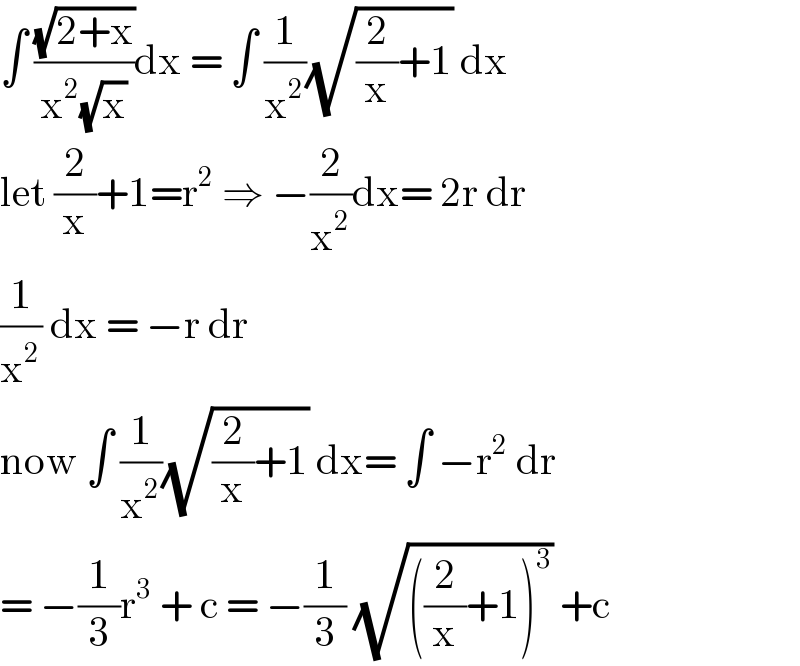
$$\int\:\frac{\sqrt{\mathrm{2}+\mathrm{x}}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}}}\mathrm{dx}\:=\:\int\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\sqrt{\frac{\mathrm{2}}{\mathrm{x}}+\mathrm{1}}\:\mathrm{dx} \\ $$$$\mathrm{let}\:\frac{\mathrm{2}}{\mathrm{x}}+\mathrm{1}=\mathrm{r}^{\mathrm{2}} \:\Rightarrow\:−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\:\mathrm{2r}\:\mathrm{dr} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=\:−\mathrm{r}\:\mathrm{dr}\: \\ $$$$\mathrm{now}\:\int\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\sqrt{\frac{\mathrm{2}}{\mathrm{x}}+\mathrm{1}}\:\mathrm{dx}=\:\int\:−\mathrm{r}^{\mathrm{2}} \:\mathrm{dr} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{r}^{\mathrm{3}} \:+\:\mathrm{c}\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\:\sqrt{\left(\frac{\mathrm{2}}{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{3}} }\:+\mathrm{c} \\ $$
Commented by petrochengula last updated on 04/Jan/20

$${you}\:{and}\:{I}\:{have}\:{been}\:{thinking}\:{about}\:{the}\:{same}\:{thing} \\ $$
Commented by jagoll last updated on 04/Jan/20

$$\mathrm{haha}…\mathrm{yes}\:\mathrm{sir} \\ $$
Commented by john santu last updated on 05/Jan/20

$${thanks}\:{both} \\ $$
Answered by petrochengula last updated on 04/Jan/20
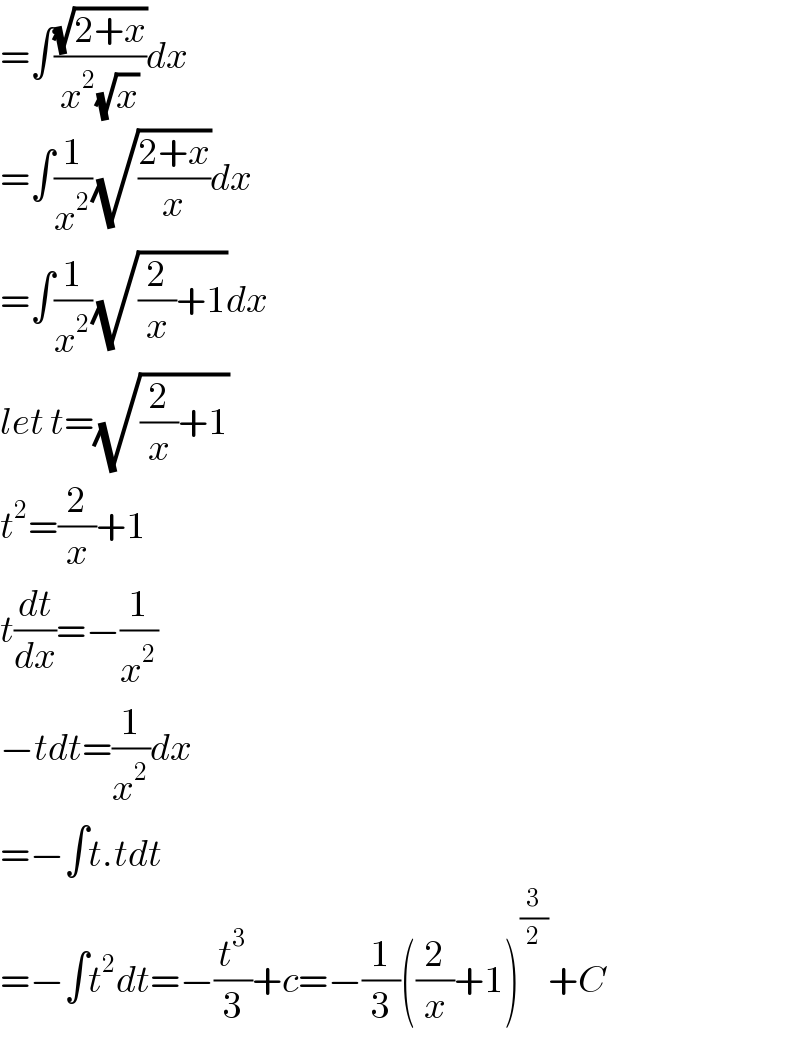
$$=\int\frac{\sqrt{\mathrm{2}+{x}}}{{x}^{\mathrm{2}} \sqrt{{x}}}{dx} \\ $$$$=\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\sqrt{\frac{\mathrm{2}+{x}}{{x}}}{dx} \\ $$$$=\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\sqrt{\frac{\mathrm{2}}{{x}}+\mathrm{1}}{dx} \\ $$$${let}\:{t}=\sqrt{\frac{\mathrm{2}}{{x}}+\mathrm{1}} \\ $$$${t}^{\mathrm{2}} =\frac{\mathrm{2}}{{x}}+\mathrm{1} \\ $$$${t}\frac{{dt}}{{dx}}=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$−{tdt}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$$=−\int{t}.{tdt} \\ $$$$=−\int{t}^{\mathrm{2}} {dt}=−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+{c}=−\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{2}}{{x}}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{C} \\ $$
