Question Number 70044 by naka3546 last updated on 30/Sep/19
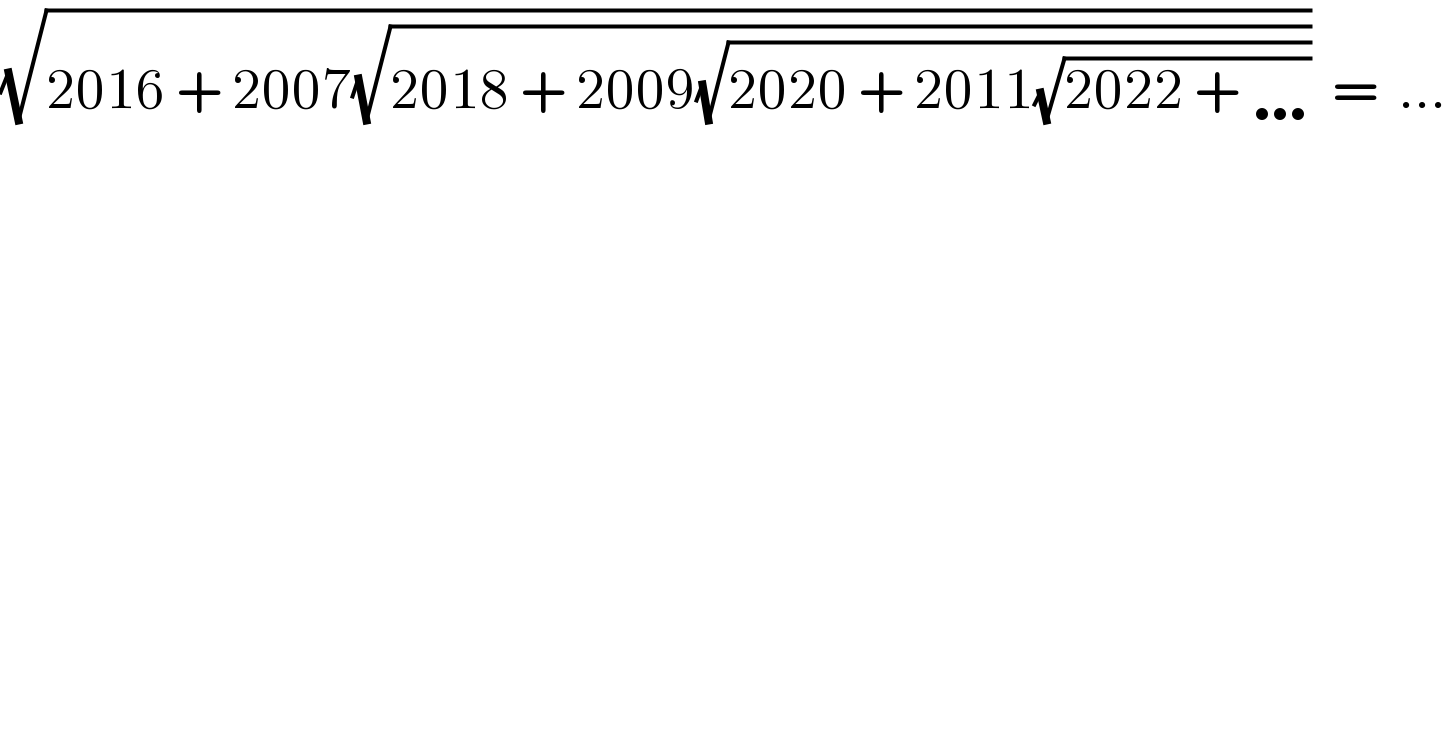
$$\sqrt{\mathrm{2016}\:+\:\mathrm{2007}\sqrt{\mathrm{2018}\:+\:\mathrm{2009}\sqrt{\mathrm{2020}\:+\:\mathrm{2011}\sqrt{\mathrm{2022}\:+\:\ldots}}}}\:\:=\:\:… \\ $$
Commented by Prithwish sen last updated on 30/Sep/19
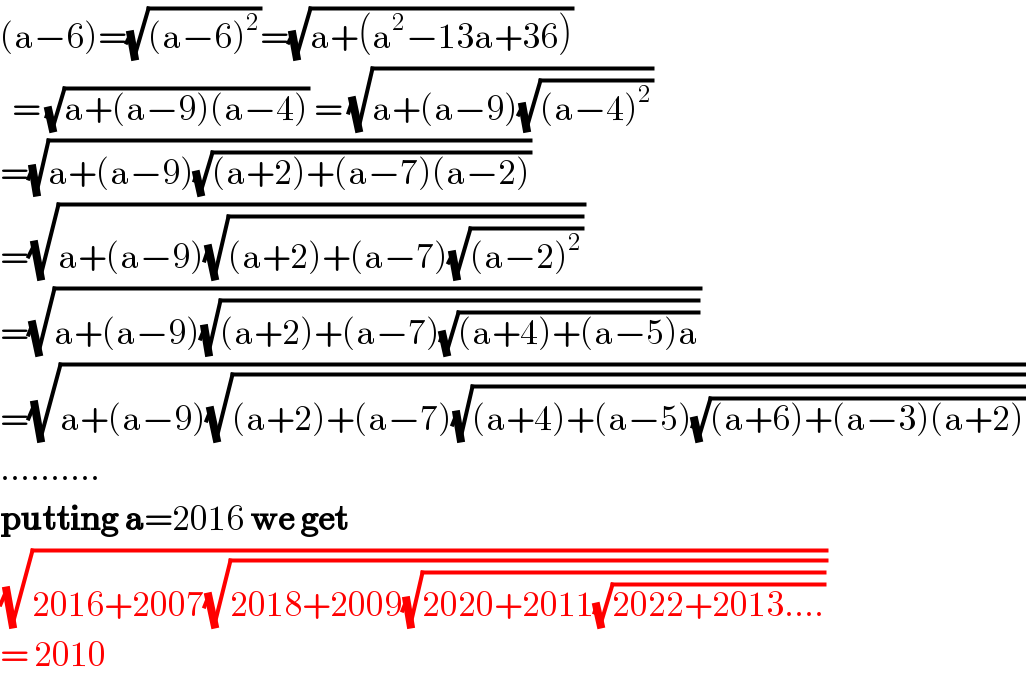
$$\left(\mathrm{a}−\mathrm{6}\right)=\sqrt{\left(\mathrm{a}−\mathrm{6}\right)^{\mathrm{2}} }=\sqrt{\mathrm{a}+\left(\mathrm{a}^{\mathrm{2}} −\mathrm{13a}+\mathrm{36}\right)} \\ $$$$\:\:=\:\sqrt{\mathrm{a}+\left(\mathrm{a}−\mathrm{9}\right)\left(\mathrm{a}−\mathrm{4}\right)}\:=\:\sqrt{\mathrm{a}+\left(\mathrm{a}−\mathrm{9}\right)\sqrt{\left(\mathrm{a}−\mathrm{4}\right)^{\mathrm{2}} }} \\ $$$$=\sqrt{\mathrm{a}+\left(\mathrm{a}−\mathrm{9}\right)\sqrt{\left(\mathrm{a}+\mathrm{2}\right)+\left(\mathrm{a}−\mathrm{7}\right)\left(\mathrm{a}−\mathrm{2}\right)}} \\ $$$$=\sqrt{\mathrm{a}+\left(\mathrm{a}−\mathrm{9}\right)\sqrt{\left(\mathrm{a}+\mathrm{2}\right)+\left(\mathrm{a}−\mathrm{7}\right)\sqrt{\left(\mathrm{a}−\mathrm{2}\right)^{\mathrm{2}} }}} \\ $$$$=\sqrt{\mathrm{a}+\left(\mathrm{a}−\mathrm{9}\right)\sqrt{\left(\mathrm{a}+\mathrm{2}\right)+\left(\mathrm{a}−\mathrm{7}\right)\sqrt{\left(\mathrm{a}+\mathrm{4}\right)+\left(\mathrm{a}−\mathrm{5}\right)\mathrm{a}}}} \\ $$$$=\sqrt{\mathrm{a}+\left(\mathrm{a}−\mathrm{9}\right)\sqrt{\left(\mathrm{a}+\mathrm{2}\right)+\left(\mathrm{a}−\mathrm{7}\right)\sqrt{\left(\mathrm{a}+\mathrm{4}\right)+\left(\mathrm{a}−\mathrm{5}\right)\sqrt{\left(\mathrm{a}+\mathrm{6}\right)+\left(\mathrm{a}−\mathrm{3}\right)\left(\mathrm{a}+\mathrm{2}\right)}}}} \\ $$$$………. \\ $$$$\boldsymbol{\mathrm{putting}}\:\boldsymbol{\mathrm{a}}=\mathrm{2016}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}} \\ $$$$\sqrt{\mathrm{2016}+\mathrm{2007}\sqrt{\mathrm{2018}+\mathrm{2009}\sqrt{\mathrm{2020}+\mathrm{2011}\sqrt{\mathrm{2022}+\mathrm{2013}….}}}} \\ $$$$=\:\mathrm{2010}\: \\ $$
