Question Number 10994 by geovane10math last updated on 06/Mar/17
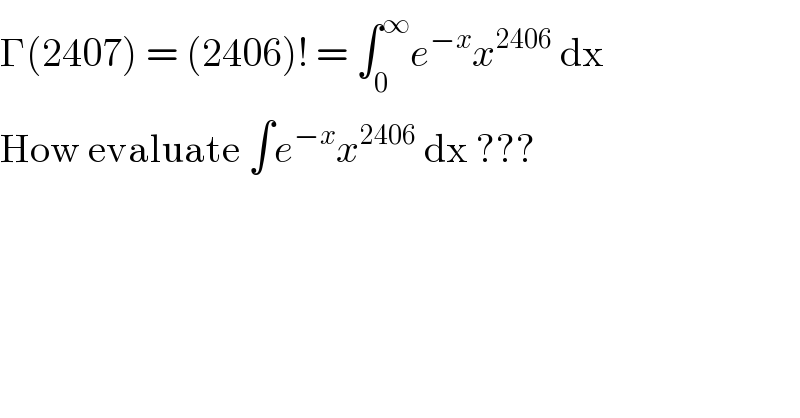
$$\Gamma\left(\mathrm{2407}\right)\:=\:\left(\mathrm{2406}\right)!\:=\:\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {x}^{\mathrm{2406}} \:\mathrm{dx} \\ $$$$\mathrm{How}\:\mathrm{evaluate}\:\int{e}^{−{x}} {x}^{\mathrm{2406}} \:\mathrm{dx}\:??? \\ $$
Commented by FilupS last updated on 06/Mar/17
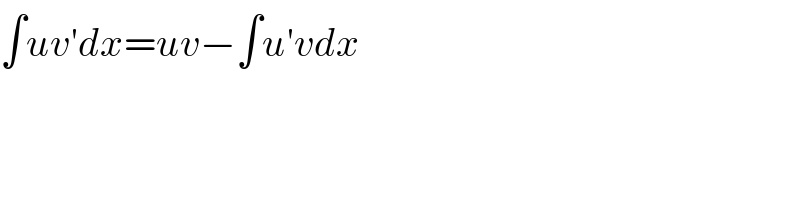
$$\int{uv}'{dx}={uv}−\int{u}'{vdx} \\ $$
Commented by FilupS last updated on 06/Mar/17
![u= x^(2406) v′=e^(−x) u′=2406x^(2405) v =−e^(−x) ∫e^(−x) x^(2406) dx=[−x^(2406) e^(−x) −2406∫−e^(−x) x^(2405) dx]_0 ^∞ repeat process for all 2406 integrals](https://www.tinkutara.com/question/Q11007.png)
$${u}=\:{x}^{\mathrm{2406}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{v}'={e}^{−{x}} \\ $$$${u}'=\mathrm{2406}{x}^{\mathrm{2405}} \:\:\:\:\:\:\:\:\:\:\:{v}\:=−{e}^{−{x}} \\ $$$$\int{e}^{−{x}} {x}^{\mathrm{2406}} \:{dx}=\left[−{x}^{\mathrm{2406}} {e}^{−{x}} −\mathrm{2406}\int−{e}^{−{x}} {x}^{\mathrm{2405}} {dx}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{repeat}\:\mathrm{process}\:\mathrm{for}\:\mathrm{all}\:\mathrm{2406}\:\mathrm{integrals} \\ $$
Commented by geovane10math last updated on 06/Mar/17

$$\mathrm{Thanks}! \\ $$
