Question Number 74129 by malwaan last updated on 19/Nov/19
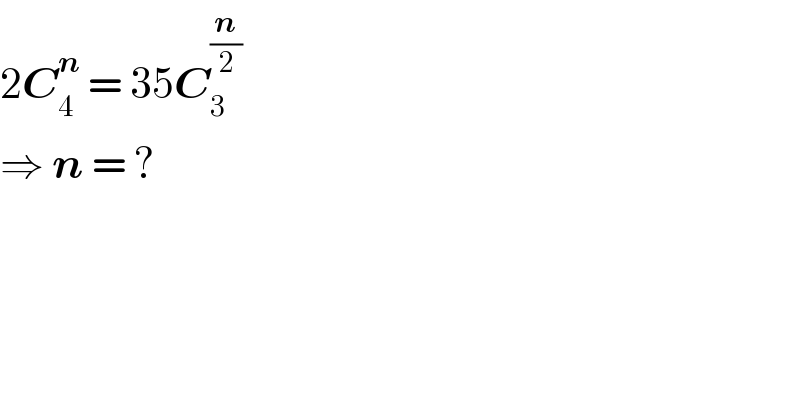
$$\mathrm{2}\boldsymbol{{C}}_{\mathrm{4}} ^{\boldsymbol{{n}}} \:=\:\mathrm{35}\boldsymbol{{C}}_{\mathrm{3}} ^{\frac{\boldsymbol{{n}}}{\mathrm{2}}} \: \\ $$$$\Rightarrow\:\boldsymbol{{n}}\:=\:? \\ $$
Answered by MJS last updated on 20/Nov/19
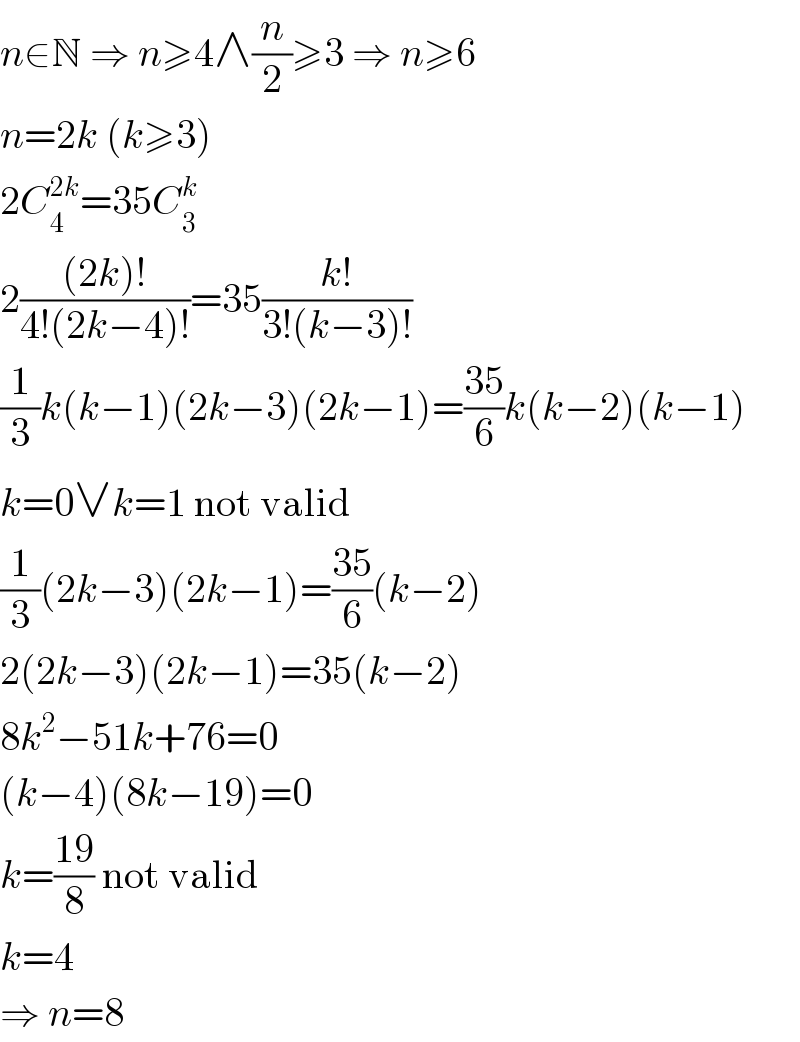
$${n}\in\mathbb{N}\:\Rightarrow\:{n}\geqslant\mathrm{4}\wedge\frac{{n}}{\mathrm{2}}\geqslant\mathrm{3}\:\Rightarrow\:{n}\geqslant\mathrm{6} \\ $$$${n}=\mathrm{2}{k}\:\left({k}\geqslant\mathrm{3}\right) \\ $$$$\mathrm{2}{C}_{\mathrm{4}} ^{\mathrm{2}{k}} =\mathrm{35}{C}_{\mathrm{3}} ^{{k}} \\ $$$$\mathrm{2}\frac{\left(\mathrm{2}{k}\right)!}{\mathrm{4}!\left(\mathrm{2}{k}−\mathrm{4}\right)!}=\mathrm{35}\frac{{k}!}{\mathrm{3}!\left({k}−\mathrm{3}\right)!} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{k}\left({k}−\mathrm{1}\right)\left(\mathrm{2}{k}−\mathrm{3}\right)\left(\mathrm{2}{k}−\mathrm{1}\right)=\frac{\mathrm{35}}{\mathrm{6}}{k}\left({k}−\mathrm{2}\right)\left({k}−\mathrm{1}\right) \\ $$$${k}=\mathrm{0}\vee{k}=\mathrm{1}\:\mathrm{not}\:\mathrm{valid} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}{k}−\mathrm{3}\right)\left(\mathrm{2}{k}−\mathrm{1}\right)=\frac{\mathrm{35}}{\mathrm{6}}\left({k}−\mathrm{2}\right) \\ $$$$\mathrm{2}\left(\mathrm{2}{k}−\mathrm{3}\right)\left(\mathrm{2}{k}−\mathrm{1}\right)=\mathrm{35}\left({k}−\mathrm{2}\right) \\ $$$$\mathrm{8}{k}^{\mathrm{2}} −\mathrm{51}{k}+\mathrm{76}=\mathrm{0} \\ $$$$\left({k}−\mathrm{4}\right)\left(\mathrm{8}{k}−\mathrm{19}\right)=\mathrm{0} \\ $$$${k}=\frac{\mathrm{19}}{\mathrm{8}}\:\mathrm{not}\:\mathrm{valid} \\ $$$${k}=\mathrm{4} \\ $$$$\Rightarrow\:{n}=\mathrm{8} \\ $$
Commented by malwaan last updated on 20/Nov/19
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{MJS} \\ $$
Commented by MJS last updated on 20/Nov/19

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
