Menu Close

2cos-x-4-cos-x-4-

Tinku Tara 0 Comments
Pin




Question Number 9029 by rzagung last updated on 15/Nov/16
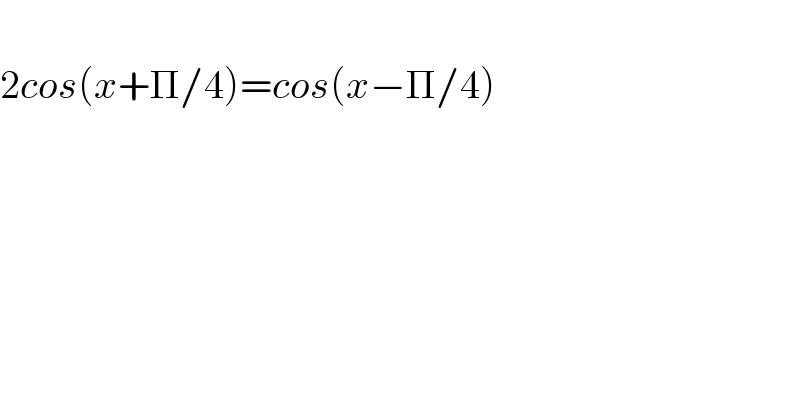
2cos(x+Π/4)=cos(x−Π/4)
$$ \\ $$$$\mathrm{2}{cos}\left({x}+\Pi/\mathrm{4}\right)={cos}\left({x}−\Pi/\mathrm{4}\right) \\ $$
Answered by Rasheed Soomro last updated on 15/Nov/16
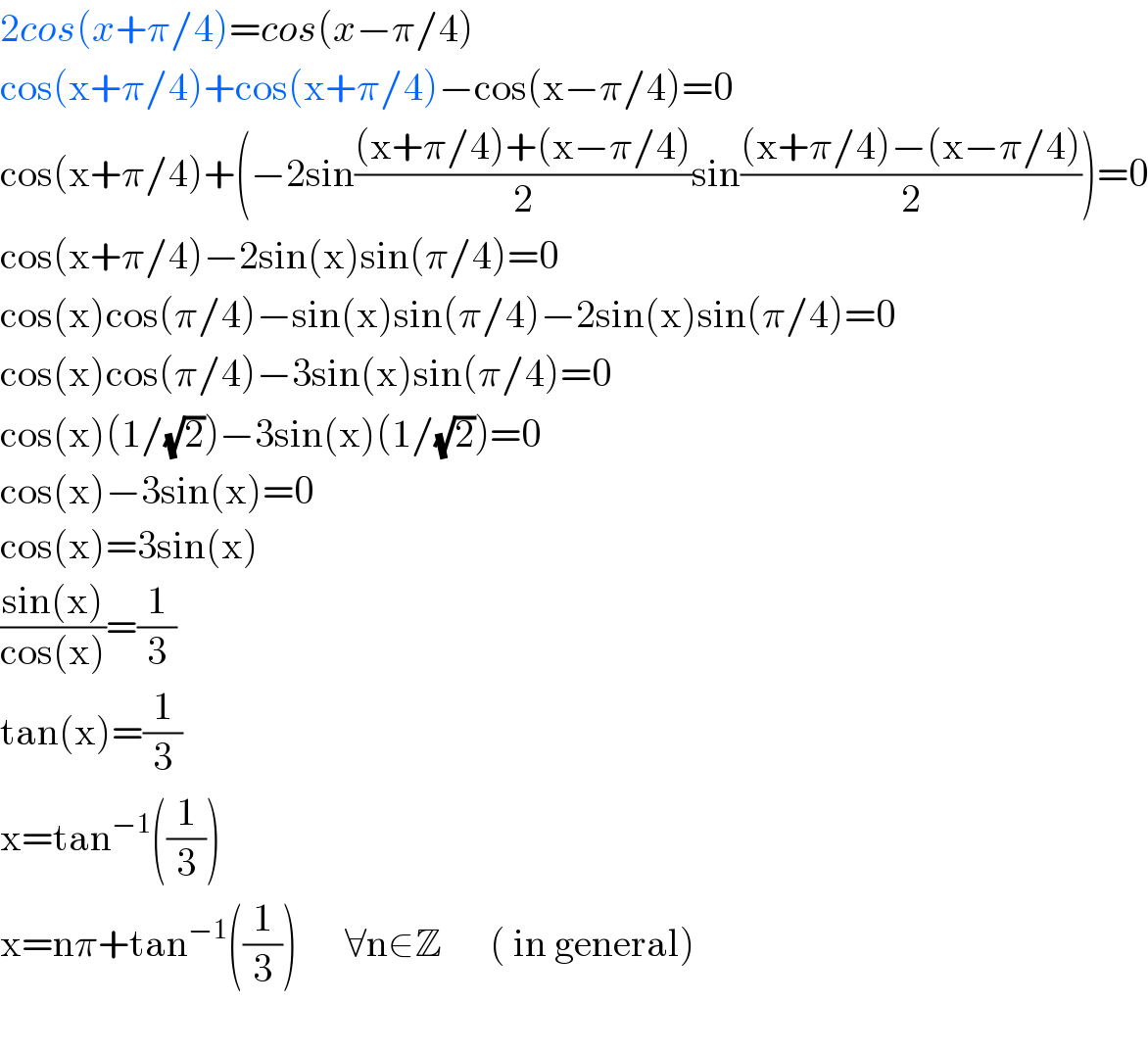
2cos(x+π/4)=cos(x−π/4) cos(x+π/4)+cos(x+π/4)−cos(x−π/4)=0 cos(x+π/4)+(−2sin(((x+π/4)+(x−π/4))/2)sin(((x+π/4)−(x−π/4))/2))=0 cos(x+π/4)−2sin(x)sin(π/4)=0 cos(x)cos(π/4)−sin(x)sin(π/4)−2sin(x)sin(π/4)=0 cos(x)cos(π/4)−3sin(x)sin(π/4)=0 cos(x)(1/(√2))−3sin(x)(1/(√2))=0 cos(x)−3sin(x)=0 cos(x)=3sin(x) ((sin(x))/(cos(x)))=(1/3) tan(x)=(1/3) x=tan^(−1) ((1/3)) x=nπ+tan^(−1) ((1/3)) ∀n∈Z ( in general)
$$\mathrm{2}{cos}\left({x}+\pi/\mathrm{4}\right)={cos}\left({x}−\pi/\mathrm{4}\right) \\ $$$$\mathrm{cos}\left(\mathrm{x}+\pi/\mathrm{4}\right)+\mathrm{cos}\left(\mathrm{x}+\pi/\mathrm{4}\right)−\mathrm{cos}\left(\mathrm{x}−\pi/\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\left(\mathrm{x}+\pi/\mathrm{4}\right)+\left(−\mathrm{2sin}\frac{\left(\mathrm{x}+\pi/\mathrm{4}\right)+\left(\mathrm{x}−\pi/\mathrm{4}\right)}{\mathrm{2}}\mathrm{sin}\frac{\left(\mathrm{x}+\pi/\mathrm{4}\right)−\left(\mathrm{x}−\pi/\mathrm{4}\right)}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\left(\mathrm{x}+\pi/\mathrm{4}\right)−\mathrm{2sin}\left(\mathrm{x}\right)\mathrm{sin}\left(\pi/\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\left(\mathrm{x}\right)\mathrm{cos}\left(\pi/\mathrm{4}\right)−\mathrm{sin}\left(\mathrm{x}\right)\mathrm{sin}\left(\pi/\mathrm{4}\right)−\mathrm{2sin}\left(\mathrm{x}\right)\mathrm{sin}\left(\pi/\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\left(\mathrm{x}\right)\mathrm{cos}\left(\pi/\mathrm{4}\right)−\mathrm{3sin}\left(\mathrm{x}\right)\mathrm{sin}\left(\pi/\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\left(\mathrm{x}\right)\left(\mathrm{1}/\sqrt{\mathrm{2}}\right)−\mathrm{3sin}\left(\mathrm{x}\right)\left(\mathrm{1}/\sqrt{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\left(\mathrm{x}\right)−\mathrm{3sin}\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\left(\mathrm{x}\right)=\mathrm{3sin}\left(\mathrm{x}\right) \\ $$$$\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{cos}\left(\mathrm{x}\right)}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{tan}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{x}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\mathrm{x}=\mathrm{n}\pi+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:\:\:\:\:\:\forall\mathrm{n}\in\mathbb{Z}\:\:\:\:\:\:\left(\:\mathrm{in}\:\mathrm{general}\right) \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 15/Nov/16
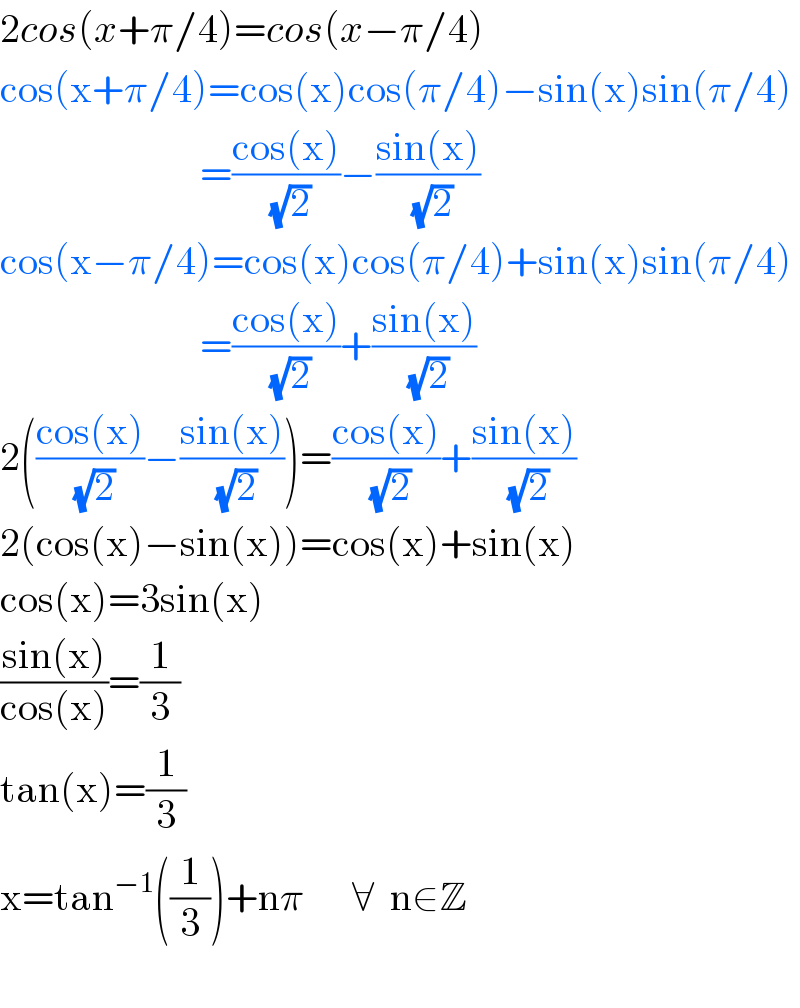
2cos(x+π/4)=cos(x−π/4) cos(x+π/4)=cos(x)cos(π/4)−sin(x)sin(π/4) =((cos(x))/( (√2)))−((sin(x))/( (√2))) cos(x−π/4)=cos(x)cos(π/4)+sin(x)sin(π/4) =((cos(x))/( (√2)))+((sin(x))/( (√2))) 2(((cos(x))/( (√2)))−((sin(x))/( (√2))))=((cos(x))/( (√2)))+((sin(x))/( (√2))) 2(cos(x)−sin(x))=cos(x)+sin(x) cos(x)=3sin(x) ((sin(x))/(cos(x)))=(1/3) tan(x)=(1/3) x=tan^(−1) ((1/3))+nπ ∀ n∈Z
$$\mathrm{2}{cos}\left({x}+\pi/\mathrm{4}\right)={cos}\left({x}−\pi/\mathrm{4}\right) \\ $$$$\mathrm{cos}\left(\mathrm{x}+\pi/\mathrm{4}\right)=\mathrm{cos}\left(\mathrm{x}\right)\mathrm{cos}\left(\pi/\mathrm{4}\right)−\mathrm{sin}\left(\mathrm{x}\right)\mathrm{sin}\left(\pi/\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{cos}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{cos}\left(\mathrm{x}−\pi/\mathrm{4}\right)=\mathrm{cos}\left(\mathrm{x}\right)\mathrm{cos}\left(\pi/\mathrm{4}\right)+\mathrm{sin}\left(\mathrm{x}\right)\mathrm{sin}\left(\pi/\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{cos}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{2}\left(\frac{\mathrm{cos}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{2}}}\right)=\frac{\mathrm{cos}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{2}\left(\mathrm{cos}\left(\mathrm{x}\right)−\mathrm{sin}\left(\mathrm{x}\right)\right)=\mathrm{cos}\left(\mathrm{x}\right)+\mathrm{sin}\left(\mathrm{x}\right) \\ $$$$\mathrm{cos}\left(\mathrm{x}\right)=\mathrm{3sin}\left(\mathrm{x}\right) \\ $$$$\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{cos}\left(\mathrm{x}\right)}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{tan}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{x}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{n}\pi\:\:\:\:\:\:\forall\:\:\mathrm{n}\in\mathbb{Z} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *