Question Number 135737 by Ar Brandon last updated on 15/Mar/21
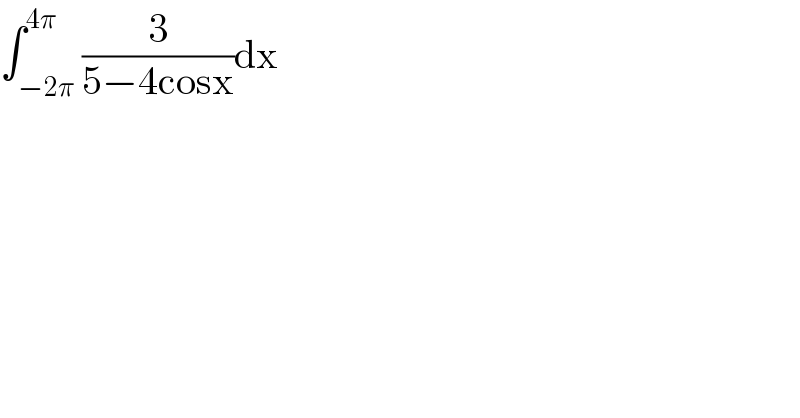
$$\int_{−\mathrm{2}\pi} ^{\mathrm{4}\pi} \frac{\mathrm{3}}{\mathrm{5}−\mathrm{4cosx}}\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 15/Mar/21
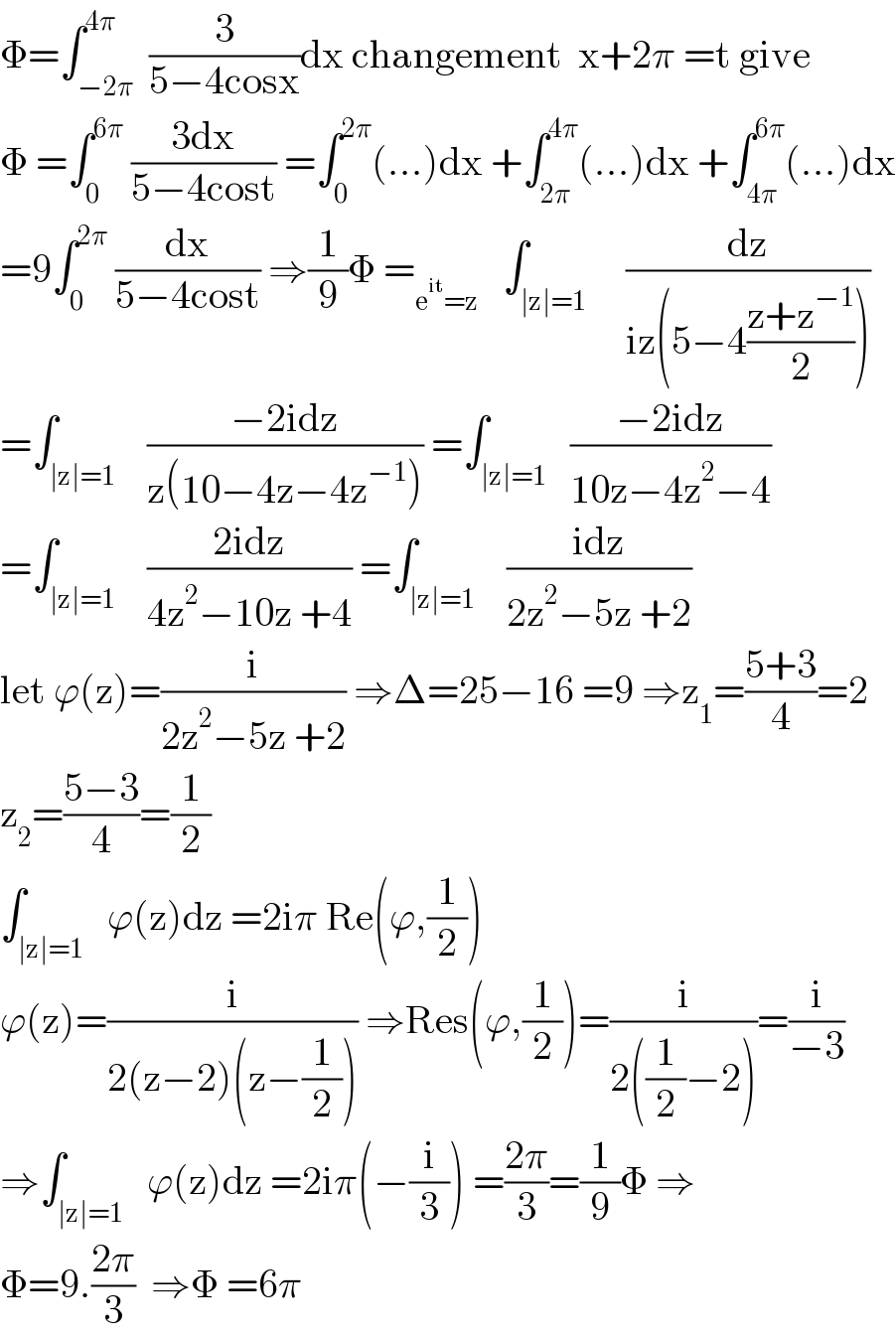
$$\Phi=\int_{−\mathrm{2}\pi} ^{\mathrm{4}\pi} \:\frac{\mathrm{3}}{\mathrm{5}−\mathrm{4cosx}}\mathrm{dx}\:\mathrm{changement}\:\:\mathrm{x}+\mathrm{2}\pi\:=\mathrm{t}\:\mathrm{give} \\ $$$$\Phi\:=\int_{\mathrm{0}} ^{\mathrm{6}\pi} \:\frac{\mathrm{3dx}}{\mathrm{5}−\mathrm{4cost}}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(…\right)\mathrm{dx}\:+\int_{\mathrm{2}\pi} ^{\mathrm{4}\pi} \left(…\right)\mathrm{dx}\:+\int_{\mathrm{4}\pi} ^{\mathrm{6}\pi} \left(…\right)\mathrm{dx} \\ $$$$=\mathrm{9}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dx}}{\mathrm{5}−\mathrm{4cost}}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{9}}\Phi\:=_{\mathrm{e}^{\mathrm{it}} =\mathrm{z}} \:\:\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{dz}}{\mathrm{iz}\left(\mathrm{5}−\mathrm{4}\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}\right)} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{−\mathrm{2idz}}{\mathrm{z}\left(\mathrm{10}−\mathrm{4z}−\mathrm{4z}^{−\mathrm{1}} \right)}\:=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{−\mathrm{2idz}}{\mathrm{10z}−\mathrm{4z}^{\mathrm{2}} −\mathrm{4}} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{2idz}}{\mathrm{4z}^{\mathrm{2}} −\mathrm{10z}\:+\mathrm{4}}\:=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{idz}}{\mathrm{2z}^{\mathrm{2}} −\mathrm{5z}\:+\mathrm{2}} \\ $$$$\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{i}}{\mathrm{2z}^{\mathrm{2}} −\mathrm{5z}\:+\mathrm{2}}\:\Rightarrow\Delta=\mathrm{25}−\mathrm{16}\:=\mathrm{9}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{5}+\mathrm{3}}{\mathrm{4}}=\mathrm{2} \\ $$$$\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{5}−\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Re}\left(\varphi,\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{i}}{\mathrm{2}\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}\right)}\:\Rightarrow\mathrm{Res}\left(\varphi,\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{i}}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)}=\frac{\mathrm{i}}{−\mathrm{3}} \\ $$$$\Rightarrow\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left(−\frac{\mathrm{i}}{\mathrm{3}}\right)\:=\frac{\mathrm{2}\pi}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{9}}\Phi\:\Rightarrow \\ $$$$\Phi=\mathrm{9}.\frac{\mathrm{2}\pi}{\mathrm{3}}\:\:\Rightarrow\Phi\:=\mathrm{6}\pi \\ $$
Answered by EDWIN88 last updated on 15/Mar/21
![via Wierrstrass subtitution tan (x/2) = z { ((dx=((2dz)/(1+z^2 )))),((cos x=((1−z^2 )/(1+z^2 )))) :} I=∫ (3/((5−((4−4z^2 )/(1+z^2 ))))) (((2dz)/(1+z^2 ))) = ∫ ((6dz)/(1+9z^2 )) let again 3z = tan θ⇒dz = ((sec^2 θ)/3) dθ I= 2∫ ((sec^2 θ)/(sec^2 θ)) dθ = 2arctan (3z) +c so ∫_(−2π) ^( 4π) (3/(5−4cos x)) dx = [ 2arctan (3tan ((x/2))) ]_(−2π) ^(4π) = 0](https://www.tinkutara.com/question/Q135755.png)
$$\mathrm{via}\:\mathrm{Wierrstrass}\:\mathrm{subtitution} \\ $$$$\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\:=\:\mathrm{z}\:\begin{cases}{\mathrm{dx}=\frac{\mathrm{2dz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }}\\{\mathrm{cos}\:\mathrm{x}=\frac{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }}\end{cases} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{3}}{\left(\mathrm{5}−\frac{\mathrm{4}−\mathrm{4z}^{\mathrm{2}} }{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\right)}\:\left(\frac{\mathrm{2dz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\right)\:=\:\int\:\frac{\mathrm{6dz}}{\mathrm{1}+\mathrm{9z}^{\mathrm{2}} } \\ $$$$\mathrm{let}\:\mathrm{again}\:\mathrm{3z}\:=\:\mathrm{tan}\:\theta\Rightarrow\mathrm{dz}\:=\:\frac{\mathrm{sec}\:^{\mathrm{2}} \theta}{\mathrm{3}}\:\mathrm{d}\theta \\ $$$$\mathrm{I}=\:\mathrm{2}\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \theta}{\mathrm{sec}\:^{\mathrm{2}} \theta}\:\mathrm{d}\theta\:=\:\mathrm{2arctan}\:\left(\mathrm{3z}\right)\:+\mathrm{c}\: \\ $$$$\mathrm{so}\:\int_{−\mathrm{2}\pi} ^{\:\mathrm{4}\pi} \frac{\mathrm{3}}{\mathrm{5}−\mathrm{4cos}\:\mathrm{x}}\:\mathrm{dx}\:=\:\left[\:\mathrm{2arctan}\:\left(\mathrm{3tan}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\:\right]_{−\mathrm{2}\pi} ^{\mathrm{4}\pi} \\ $$$$=\:\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 15/Mar/21
![answer not coreect no bijection in [−2π,4π]..!](https://www.tinkutara.com/question/Q135763.png)
$$\mathrm{answer}\:\mathrm{not}\:\mathrm{coreect}\:\mathrm{no}\:\mathrm{bijection}\:\mathrm{in}\:\left[−\mathrm{2}\pi,\mathrm{4}\pi\right]..! \\ $$
