Question Number 138863 by bramlexs22 last updated on 19/Apr/21
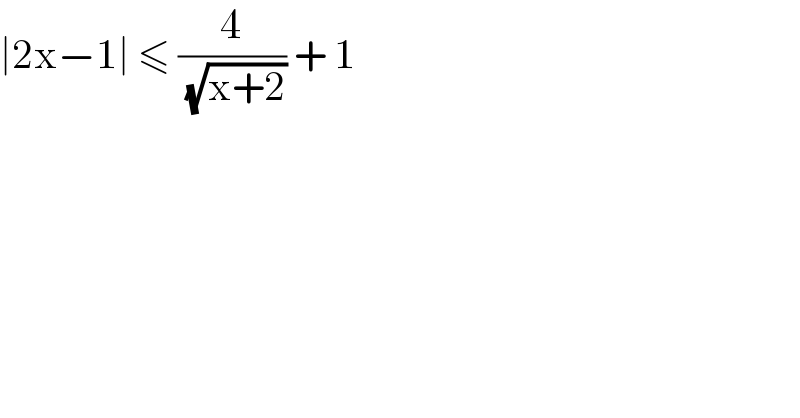
$$\mid\mathrm{2x}−\mathrm{1}\mid\:\leqslant\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{x}+\mathrm{2}}}\:+\:\mathrm{1} \\ $$
Answered by lyubita last updated on 19/Apr/21

$$-\:\mathrm{2}\:<\:{x}\:\leqslant\:\mathrm{2} \\ $$
Commented by bramlexs22 last updated on 19/Apr/21

$$\mathrm{by}\:\mathrm{Geogebra} \\ $$
Commented by bramlexs22 last updated on 19/Apr/21
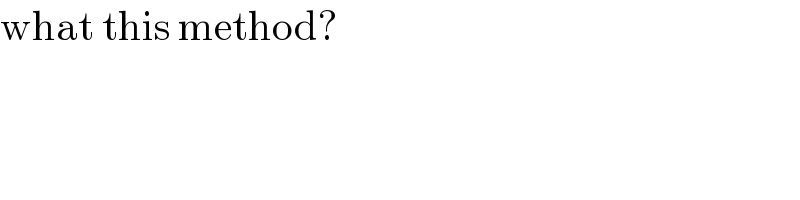
$$\mathrm{what}\:\mathrm{this}\:\mathrm{method}? \\ $$
Answered by EDWIN88 last updated on 19/Apr/21
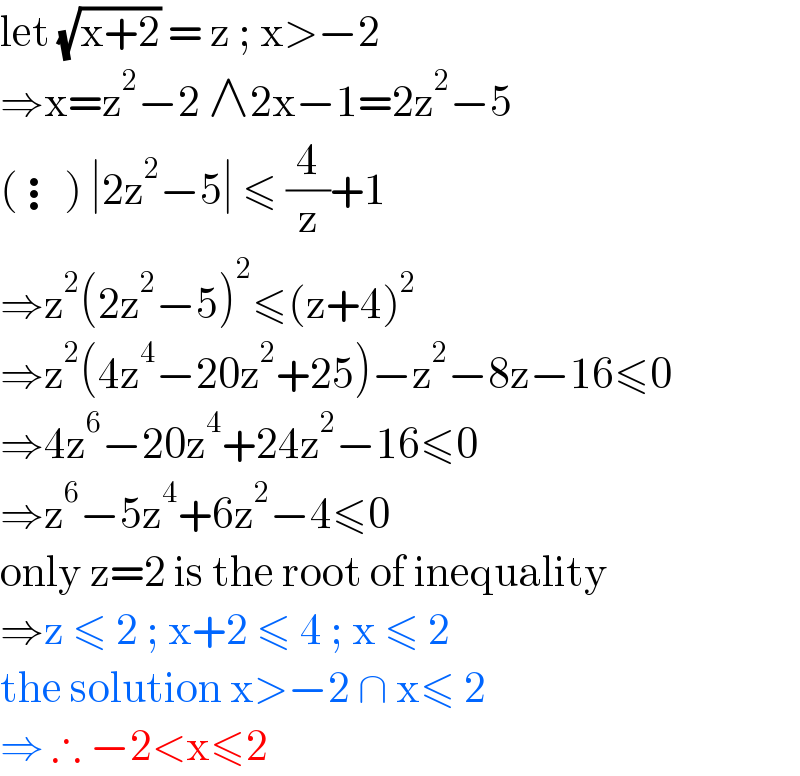
$$\mathrm{let}\:\sqrt{\mathrm{x}+\mathrm{2}}\:=\:\mathrm{z}\:;\:\mathrm{x}>−\mathrm{2} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{z}^{\mathrm{2}} −\mathrm{2}\:\wedge\mathrm{2x}−\mathrm{1}=\mathrm{2z}^{\mathrm{2}} −\mathrm{5} \\ $$$$\left(\vdots\right)\:\mid\mathrm{2z}^{\mathrm{2}} −\mathrm{5}\mid\:\leqslant\:\frac{\mathrm{4}}{\mathrm{z}}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{z}^{\mathrm{2}} \left(\mathrm{2z}^{\mathrm{2}} −\mathrm{5}\right)^{\mathrm{2}} \leqslant\left(\mathrm{z}+\mathrm{4}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{z}^{\mathrm{2}} \left(\mathrm{4z}^{\mathrm{4}} −\mathrm{20z}^{\mathrm{2}} +\mathrm{25}\right)−\mathrm{z}^{\mathrm{2}} −\mathrm{8z}−\mathrm{16}\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{4z}^{\mathrm{6}} −\mathrm{20z}^{\mathrm{4}} +\mathrm{24z}^{\mathrm{2}} −\mathrm{16}\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{z}^{\mathrm{6}} −\mathrm{5z}^{\mathrm{4}} +\mathrm{6z}^{\mathrm{2}} −\mathrm{4}\leqslant\mathrm{0} \\ $$$$\mathrm{only}\:\mathrm{z}=\mathrm{2}\:\mathrm{is}\:\mathrm{the}\:\mathrm{root}\:\mathrm{of}\:\mathrm{inequality} \\ $$$$\Rightarrow\mathrm{z}\:\leqslant\:\mathrm{2}\:;\:\mathrm{x}+\mathrm{2}\:\leqslant\:\mathrm{4}\:;\:\mathrm{x}\:\leqslant\:\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{x}>−\mathrm{2}\:\cap\:\mathrm{x}\leqslant\:\mathrm{2}\: \\ $$$$\Rightarrow\:\therefore\:−\mathrm{2}<\mathrm{x}\leqslant\mathrm{2} \\ $$
