Menu Close

2x-2-1-2x-x-2-1-x-2-x-x-1-x-2-1-dx-dx-x-x-1-1-x-3-

Tinku Tara 0 Comments
Pin




Question Number 73202 by MJS last updated on 08/Nov/19
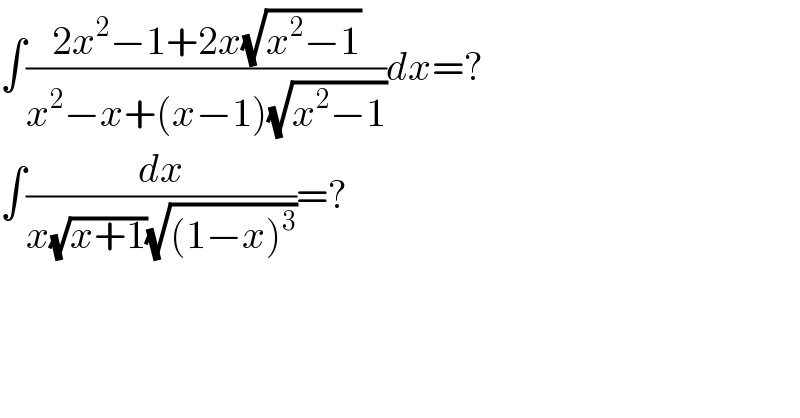
∫((2x^2 −1+2x(√(x^2 −1)))/(x^2 −x+(x−1)(√(x^2 −1))))dx=? ∫(dx/(x(√(x+1))(√((1−x)^3 ))))=?
$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}+\mathrm{2}{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}^{\mathrm{2}} −{x}+\left({x}−\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{dx}=? \\ $$$$\int\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}\sqrt{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }}=? \\ $$
Commented by mathmax by abdo last updated on 09/Nov/19
let A =∫ (dx/(x(√(x+1))(1−x)^(3/2) )) changement x=cos2t give A =∫ ((−2sin(2t) dt)/(cos(2t)(√(2cos^2 t))(2sin^2 t)^(3/2) )) =−2 ∫ ((sin(2t)dt)/(cos(2t)(√2)cost 2^(3/2) sin^3 t)) =−2 ∫ ((2sint cost)/(4 cos(2t)cost sint sin^2 t))dt =−∫ (dt/(cos(2t)(((1−cos(2t))/2)))) =−2 ∫ (dt/(cos(2t)−cos^2 (2t))) =−2 ∫ (dt/(cos(2t)−((1+cos(4t))/2))) =−4 ∫ (dt/(2cos(2t)−cos(4t)−1)) =_(2t=z) −4 ∫ (dz/(2(2cos(z)−cos(2z)−1))) =−2 ∫ (dz/(2cosz −cos(2z)−1)) =−2 ∫ (dz/(2cos(z)−(2cos^2 z−1)−1)) =−2 ∫ (dz/(−2cos^2 z+2cosz)) =∫ (dz/(cos^2 z −cosz)) =∫ (dz/(cosz(cosz−1))) =∫ ((1/(cosz−1))−(1/(cosz)))dz =∫ (dz/(cosz−1))−∫ (dz/(cosz)) we have ∫ (dz/(cosz−1)) =_(tan((z/2))=u) ∫ (1/(((1−u^2 )/(1+u^2 ))−1))((2du)/(1+u^2 )) =∫ ((2du)/(1−u^2 −1−u^2 )) =∫− (du/u^2 ) =(1/u) +C =(1/(tan((z/2)))) +c =(1/(tan(t))) +C =(1/(tan(((arcosx)/2)))) +C also ∫ (dz/(cosz)) =_(tan((z/2))=u) ∫ (1/((1−u^2 )/(1+u^2 )))((2du)/(1+u^2 )) =∫ ((2du)/(1−u^2 )) =∫((1/(1+u))+(1/(1−u)))du =ln∣((1+u)/(1−u))∣ +c =ln∣((1+tan((z/2)))/(1−tan((z/2))))∣ +c =ln∣((1+tan(t))/(1−tan(t)))∣ +c =ln∣((1+tan(((arcosx)/2)))/(1−tan(((arcosx)/2))))∣ +c ⇒ A =(1/(tan(((arcosx)/2)))) −ln∣((1+tan(((arcosx)/2)))/(1−tan(((arcosx)/2))))∣ +C .
$${let}\:{A}\:=\int\:\:\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{changement}\:{x}={cos}\mathrm{2}{t}\:{give} \\ $$$${A}\:=\int\:\:\frac{−\mathrm{2}{sin}\left(\mathrm{2}{t}\right)\:{dt}}{{cos}\left(\mathrm{2}{t}\right)\sqrt{\mathrm{2}{cos}^{\mathrm{2}} {t}}\left(\mathrm{2}{sin}^{\mathrm{2}} {t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=−\mathrm{2}\:\int\:\:\:\frac{{sin}\left(\mathrm{2}{t}\right){dt}}{{cos}\left(\mathrm{2}{t}\right)\sqrt{\mathrm{2}}{cost}\:\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \:{sin}^{\mathrm{3}} {t}} \\ $$$$=−\mathrm{2}\:\int\:\:\frac{\mathrm{2}{sint}\:{cost}}{\mathrm{4}\:{cos}\left(\mathrm{2}{t}\right){cost}\:{sint}\:{sin}^{\mathrm{2}} {t}}{dt} \\ $$$$=−\int\:\:\frac{{dt}}{{cos}\left(\mathrm{2}{t}\right)\left(\frac{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right)}\:=−\mathrm{2}\:\int\:\:\:\frac{{dt}}{{cos}\left(\mathrm{2}{t}\right)−{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)} \\ $$$$=−\mathrm{2}\:\int\:\:\frac{{dt}}{{cos}\left(\mathrm{2}{t}\right)−\frac{\mathrm{1}+{cos}\left(\mathrm{4}{t}\right)}{\mathrm{2}}}\:=−\mathrm{4}\:\int\:\:\:\frac{{dt}}{\mathrm{2}{cos}\left(\mathrm{2}{t}\right)−{cos}\left(\mathrm{4}{t}\right)−\mathrm{1}} \\ $$$$=_{\mathrm{2}{t}={z}} \:\:\:\:−\mathrm{4}\:\int\:\:\:\:\frac{{dz}}{\mathrm{2}\left(\mathrm{2}{cos}\left({z}\right)−{cos}\left(\mathrm{2}{z}\right)−\mathrm{1}\right)} \\ $$$$=−\mathrm{2}\:\int\:\:\:\:\frac{{dz}}{\mathrm{2}{cosz}\:−{cos}\left(\mathrm{2}{z}\right)−\mathrm{1}} \\ $$$$=−\mathrm{2}\:\int\:\:\frac{{dz}}{\mathrm{2}{cos}\left({z}\right)−\left(\mathrm{2}{cos}^{\mathrm{2}} {z}−\mathrm{1}\right)−\mathrm{1}} \\ $$$$=−\mathrm{2}\:\int\:\:\frac{{dz}}{−\mathrm{2}{cos}^{\mathrm{2}} {z}+\mathrm{2}{cosz}}\:=\int\:\:\frac{{dz}}{{cos}^{\mathrm{2}} {z}\:−{cosz}} \\ $$$$=\int\:\:\frac{{dz}}{{cosz}\left({cosz}−\mathrm{1}\right)}\:=\int\:\left(\frac{\mathrm{1}}{{cosz}−\mathrm{1}}−\frac{\mathrm{1}}{{cosz}}\right){dz} \\ $$$$=\int\:\:\frac{{dz}}{{cosz}−\mathrm{1}}−\int\:\:\frac{{dz}}{{cosz}}\:{we}\:{have} \\ $$$$\int\:\:\frac{{dz}}{{cosz}−\mathrm{1}}\:=_{{tan}\left(\frac{{z}}{\mathrm{2}}\right)={u}} \:\:\:\int\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }−\mathrm{1}}\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\int\:\:\:\frac{\mathrm{2}{du}}{\mathrm{1}−{u}^{\mathrm{2}} −\mathrm{1}−{u}^{\mathrm{2}} }\:=\int−\:\frac{{du}}{{u}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{u}}\:+{C}\:=\frac{\mathrm{1}}{{tan}\left(\frac{{z}}{\mathrm{2}}\right)}\:+{c} \\ $$$$=\frac{\mathrm{1}}{{tan}\left({t}\right)}\:+{C}\:=\frac{\mathrm{1}}{{tan}\left(\frac{{arcosx}}{\mathrm{2}}\right)}\:+{C}\:\:{also} \\ $$$$\int\:\:\frac{{dz}}{{cosz}}\:=_{{tan}\left(\frac{{z}}{\mathrm{2}}\right)={u}} \:\:\int\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{2}{du}}{\mathrm{1}−{u}^{\mathrm{2}} }\:=\int\left(\frac{\mathrm{1}}{\mathrm{1}+{u}}+\frac{\mathrm{1}}{\mathrm{1}−{u}}\right){du} \\ $$$$={ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\:+{c}\:={ln}\mid\frac{\mathrm{1}+{tan}\left(\frac{{z}}{\mathrm{2}}\right)}{\mathrm{1}−{tan}\left(\frac{{z}}{\mathrm{2}}\right)}\mid\:+{c}\:={ln}\mid\frac{\mathrm{1}+{tan}\left({t}\right)}{\mathrm{1}−{tan}\left({t}\right)}\mid\:+{c} \\ $$$$={ln}\mid\frac{\mathrm{1}+{tan}\left(\frac{{arcosx}}{\mathrm{2}}\right)}{\mathrm{1}−{tan}\left(\frac{{arcosx}}{\mathrm{2}}\right)}\mid\:+{c}\:\Rightarrow \\ $$$${A}\:=\frac{\mathrm{1}}{{tan}\left(\frac{{arcosx}}{\mathrm{2}}\right)}\:−{ln}\mid\frac{\mathrm{1}+{tan}\left(\frac{{arcosx}}{\mathrm{2}}\right)}{\mathrm{1}−{tan}\left(\frac{{arcosx}}{\mathrm{2}}\right)}\mid\:+{C}\:. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 10/Nov/19
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathmax by abdo last updated on 10/Nov/19
you are welcome.
$${you}\:{are}\:{welcome}. \\ $$
Answered by MJS last updated on 10/Nov/19
∫(dx/(x(√(x+1))(√((1−x)^3 ))))= [t=((√(1+x))/( (√(1−x)))) → dx=(√(x+1))(√((1−x)^3 ))dt] =∫((t^2 +1)/(t^2 −1))dt= =∫dt+∫(dt/(t−1))−∫(dt/(t+1))= =t+ln ((t−1)/(t+1)) =((√(1+x))/( (√(1−x))))+ln ((1−(√(1−x^2 )))/x) +C
$$\int\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}\sqrt{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{1}+{x}}}{\:\sqrt{\mathrm{1}−{x}}}\:\rightarrow\:{dx}=\sqrt{{x}+\mathrm{1}}\sqrt{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }{dt}\right] \\ $$$$=\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}= \\ $$$$=\int{dt}+\int\frac{{dt}}{{t}−\mathrm{1}}−\int\frac{{dt}}{{t}+\mathrm{1}}= \\ $$$$={t}+\mathrm{ln}\:\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\:=\frac{\sqrt{\mathrm{1}+{x}}}{\:\sqrt{\mathrm{1}−{x}}}+\mathrm{ln}\:\frac{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:+{C} \\ $$
Answered by MJS last updated on 10/Nov/19
∫((2x^2 −1+2x(√(x^2 −1)))/(x^2 −x+(x−1)(√(x^2 −1))))dx= [t=x+(√(x^2 −1)) → dx=((√(x^2 −1))/(x+(√(x^2 −1))))dt] =∫((t+1)/(t−1))dt=t+2ln (t−1) = =x+(√(x^2 −1))+2ln ∣x−1+(√(x^2 −1))∣ +C
$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}+\mathrm{2}{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}^{\mathrm{2}} −{x}+\left({x}−\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{dt}\right] \\ $$$$=\int\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}{dt}={t}+\mathrm{2ln}\:\left({t}−\mathrm{1}\right)\:= \\ $$$$={x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}+\mathrm{2ln}\:\mid{x}−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\mid\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *