Menu Close

2x-2-3x-4-4x-3-5-dx-

Tinku Tara
Pin




Question Number 65869 by Rio Michael last updated on 05/Aug/19
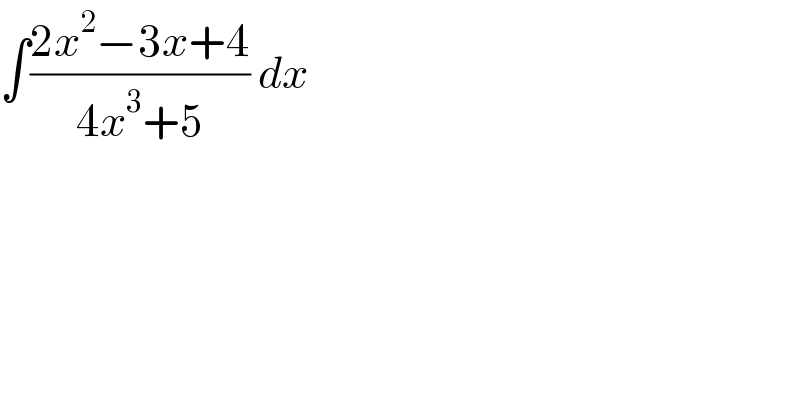
∫((2x^2 −3x+4)/(4x^3 +5)) dx
$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}}{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{5}}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 05/Aug/19
let I =∫ ((2x^2 −3x+4)/(4x^3 +5))dx ⇒ I =∫ ((2x^2 −3x+4)/(4(x^3 +(5/4))))dx =(1/4)∫ ((2x^2 −3x+4)/(x^3 +^3 ((√(5/4)))^3 )) (let put^3 (√(5/4))=α) =(1/4)∫ ((2x^2 −3x+5)/((x+α)(x^2 −αx +α^2 )))dt let decompose F(x) =((2x^2 −3x+5)/((x+α)(x^2 −αx +α^2 ))) ⇒F(x) =(a/(x+α)) +((bx+c)/(x^2 −αx +α^2 )) a =lim_(x→−α) (x+α)F(x) =((2α^2 −3α +5)/(3α^2 )) lim_(x→+∞) xF(x) =(1/2) =a+b ⇒b =(1/2)−((2α^2 −3α+5)/(3α^2 )) =((3α^2 −4α^2 +6α−10)/(6α^2 )) =((−α^2 +6α −10)/(6α^2 )) F(0) =(4/5) =(a/α) +(c/α^2 ) ⇒(4/5)α^2 =aα+c ⇒c =(4/5) −aα the coefficients are known ⇒∫ F(x)dx =a ln∣x+α∣ +(b/2) ∫ ((2x−α +α)/(x^2 −αx +α^2 ))dx +c ∫ (dx/(x^2 −αx +α^2 )) =aln∣x+α∣+(b/2)ln(x^2 −αx +α^2 ) +(((bα)/2)+c)∫ (dx/(x^2 −αx +α^2 )) =....
$${let}\:{I}\:=\int\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}}{\mathrm{4}{x}^{\mathrm{3}} \:+\mathrm{5}}{dx}\:\Rightarrow\:{I}\:=\int\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}}{\mathrm{4}\left({x}^{\mathrm{3}} \:+\frac{\mathrm{5}}{\mathrm{4}}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}}{{x}^{\mathrm{3}} +^{\mathrm{3}} \left(\sqrt{\frac{\mathrm{5}}{\mathrm{4}}}\right)^{\mathrm{3}} }\:\:\:\:\:\left({let}\:{put}\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}}{\mathrm{4}}}=\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{5}}{\left({x}+\alpha\right)\left({x}^{\mathrm{2}} −\alpha{x}\:+\alpha^{\mathrm{2}} \right)}{dt}\:\:{let}\:{decompose}\: \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{5}}{\left({x}+\alpha\right)\left({x}^{\mathrm{2}} −\alpha{x}\:+\alpha^{\mathrm{2}} \right)}\:\Rightarrow{F}\left({x}\right)\:=\frac{{a}}{{x}+\alpha}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} −\alpha{x}\:+\alpha^{\mathrm{2}} } \\ $$$${a}\:={lim}_{{x}\rightarrow−\alpha} \left({x}+\alpha\right){F}\left({x}\right)\:=\frac{\mathrm{2}\alpha^{\mathrm{2}} −\mathrm{3}\alpha\:+\mathrm{5}}{\mathrm{3}\alpha^{\mathrm{2}} } \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:={a}+{b}\:\Rightarrow{b}\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{2}\alpha^{\mathrm{2}} −\mathrm{3}\alpha+\mathrm{5}}{\mathrm{3}\alpha^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{3}\alpha^{\mathrm{2}} −\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{6}\alpha−\mathrm{10}}{\mathrm{6}\alpha^{\mathrm{2}} }\:=\frac{−\alpha^{\mathrm{2}} \:+\mathrm{6}\alpha\:−\mathrm{10}}{\mathrm{6}\alpha^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)\:=\frac{\mathrm{4}}{\mathrm{5}}\:=\frac{{a}}{\alpha}\:+\frac{{c}}{\alpha^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{4}}{\mathrm{5}}\alpha^{\mathrm{2}} ={a}\alpha+{c}\:\Rightarrow{c}\:=\frac{\mathrm{4}}{\mathrm{5}}\:−{a}\alpha\:\:{the}\:{coefficients} \\ $$$${are}\:{known}\:\Rightarrow\int\:{F}\left({x}\right){dx}\:={a}\:{ln}\mid{x}+\alpha\mid\:+\frac{{b}}{\mathrm{2}}\:\int\:\frac{\mathrm{2}{x}−\alpha\:+\alpha}{{x}^{\mathrm{2}} −\alpha{x}\:+\alpha^{\mathrm{2}} }{dx} \\ $$$$+{c}\:\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\alpha{x}\:+\alpha^{\mathrm{2}} }\:={aln}\mid{x}+\alpha\mid+\frac{{b}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} −\alpha{x}\:+\alpha^{\mathrm{2}} \right) \\ $$$$+\left(\frac{{b}\alpha}{\mathrm{2}}+{c}\right)\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\alpha{x}\:+\alpha^{\mathrm{2}} }\:=…. \\ $$$$ \\ $$
Answered by MJS last updated on 05/Aug/19
∫((2x^2 −3x+4)/(4x^3 +5))dx=(1/2)∫((x^2 −(3/2)x+2)/(x^3 +(5/4)))dx= [a=−(3/2); b=2; c=((5/4))^(1/3) ] =(1/2)∫((x^2 +ax+b)/(x^3 +c^3 ))dx ∫((x^2 +ax+b)/(x^3 +c^3 ))dx=∫((x^2 +ax+b)/((x+c)(x^2 −cx+c^2 )))dx= =−((ac−b−c^2 )/(3c^2 ))∫(dx/(x+c))+(1/(3c^2 ))∫(((ac−b+2c^2 )x+(ac+2b−c^2 )c)/(x^2 −cx+c^2 ))dx the first one −((ac−b−c^2 )/(3c^2 ))∫(dx/(x+c))=−((ac−b−c^2 )/(3c^2 ))ln (x+c) the second one (1/(3c^2 ))∫(((ac−b+2c^2 )x+(ac+2b−c^2 )c)/(x^2 −cx+c^2 ))dx= [α=ac−b+2c^2 ; β=(ac+2b−c^2 )c] =(1/(3c^2 ))∫((αx+β)/(x^2 −cx+c^2 ))dx ∫((αx+β)/(x^2 −cx+c^2 ))dx= =((cα+2β)/2)∫(dx/(x^2 −cx+c^2 ))+(α/2)∫((2x−c)/(x^2 −cx+c^2 ))dx= =(((cα+2β)(√3))/(3c))arctan (((2x−c)(√3))/(3c)) +(α/2)ln (x^2 −cx+c^2 ) now going backwards... a=−(3/2); b=2; c=((5/4))^(1/3) α=ac−b+2c^2 ; β=(ac+2b−c^2 )c α=−2−(3/4)((10))^(1/3) +(1/2)((100))^(1/3) β=−(5/4)+2((10))^(1/3) −(3/8)((100))^(1/3) ... please do this work for yourself
$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}}{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{5}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}{x}+\mathrm{2}}{{x}^{\mathrm{3}} +\frac{\mathrm{5}}{\mathrm{4}}}{dx}= \\ $$$$\:\:\:\:\:\left[{a}=−\frac{\mathrm{3}}{\mathrm{2}};\:{b}=\mathrm{2};\:{c}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{5}}{\mathrm{4}}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} +{ax}+{b}}{{x}^{\mathrm{3}} +{c}^{\mathrm{3}} }{dx} \\ $$$$\int\frac{{x}^{\mathrm{2}} +{ax}+{b}}{{x}^{\mathrm{3}} +{c}^{\mathrm{3}} }{dx}=\int\frac{{x}^{\mathrm{2}} +{ax}+{b}}{\left({x}+{c}\right)\left({x}^{\mathrm{2}} −{cx}+{c}^{\mathrm{2}} \right)}{dx}= \\ $$$$=−\frac{{ac}−{b}−{c}^{\mathrm{2}} }{\mathrm{3}{c}^{\mathrm{2}} }\int\frac{{dx}}{{x}+{c}}+\frac{\mathrm{1}}{\mathrm{3}{c}^{\mathrm{2}} }\int\frac{\left({ac}−{b}+\mathrm{2}{c}^{\mathrm{2}} \right){x}+\left({ac}+\mathrm{2}{b}−{c}^{\mathrm{2}} \right){c}}{{x}^{\mathrm{2}} −{cx}+{c}^{\mathrm{2}} }{dx} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{one} \\ $$$$−\frac{{ac}−{b}−{c}^{\mathrm{2}} }{\mathrm{3}{c}^{\mathrm{2}} }\int\frac{{dx}}{{x}+{c}}=−\frac{{ac}−{b}−{c}^{\mathrm{2}} }{\mathrm{3}{c}^{\mathrm{2}} }\mathrm{ln}\:\left({x}+{c}\right) \\ $$$$\mathrm{the}\:\mathrm{second}\:\mathrm{one} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}{c}^{\mathrm{2}} }\int\frac{\left({ac}−{b}+\mathrm{2}{c}^{\mathrm{2}} \right){x}+\left({ac}+\mathrm{2}{b}−{c}^{\mathrm{2}} \right){c}}{{x}^{\mathrm{2}} −{cx}+{c}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[\alpha={ac}−{b}+\mathrm{2}{c}^{\mathrm{2}} ;\:\beta=\left({ac}+\mathrm{2}{b}−{c}^{\mathrm{2}} \right){c}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{c}^{\mathrm{2}} }\int\frac{\alpha{x}+\beta}{{x}^{\mathrm{2}} −{cx}+{c}^{\mathrm{2}} }{dx} \\ $$$$\int\frac{\alpha{x}+\beta}{{x}^{\mathrm{2}} −{cx}+{c}^{\mathrm{2}} }{dx}= \\ $$$$=\frac{{c}\alpha+\mathrm{2}\beta}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{cx}+{c}^{\mathrm{2}} }+\frac{\alpha}{\mathrm{2}}\int\frac{\mathrm{2}{x}−{c}}{{x}^{\mathrm{2}} −{cx}+{c}^{\mathrm{2}} }{dx}= \\ $$$$=\frac{\left({c}\alpha+\mathrm{2}\beta\right)\sqrt{\mathrm{3}}}{\mathrm{3}{c}}\mathrm{arctan}\:\frac{\left(\mathrm{2}{x}−{c}\right)\sqrt{\mathrm{3}}}{\mathrm{3}{c}}\:+\frac{\alpha}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{cx}+{c}^{\mathrm{2}} \right) \\ $$$$\mathrm{now}\:\mathrm{going}\:\mathrm{backwards}… \\ $$$${a}=−\frac{\mathrm{3}}{\mathrm{2}};\:{b}=\mathrm{2};\:{c}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{5}}{\mathrm{4}}} \\ $$$$\alpha={ac}−{b}+\mathrm{2}{c}^{\mathrm{2}} ;\:\beta=\left({ac}+\mathrm{2}{b}−{c}^{\mathrm{2}} \right){c} \\ $$$$\alpha=−\mathrm{2}−\frac{\mathrm{3}}{\mathrm{4}}\sqrt[{\mathrm{3}}]{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\mathrm{100}} \\ $$$$\beta=−\frac{\mathrm{5}}{\mathrm{4}}+\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{10}}−\frac{\mathrm{3}}{\mathrm{8}}\sqrt[{\mathrm{3}}]{\mathrm{100}} \\ $$$$… \\ $$$$\mathrm{please}\:\mathrm{do}\:\mathrm{this}\:\mathrm{work}\:\mathrm{for}\:\mathrm{yourself} \\ $$
Commented by mathmax by abdo last updated on 05/Aug/19
thank you sir mjs
$${thank}\:{you}\:{sir}\:{mjs} \\ $$

Pin