Menu Close

2x-3-1-x-4-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 77960 by jagoll last updated on 12/Jan/20
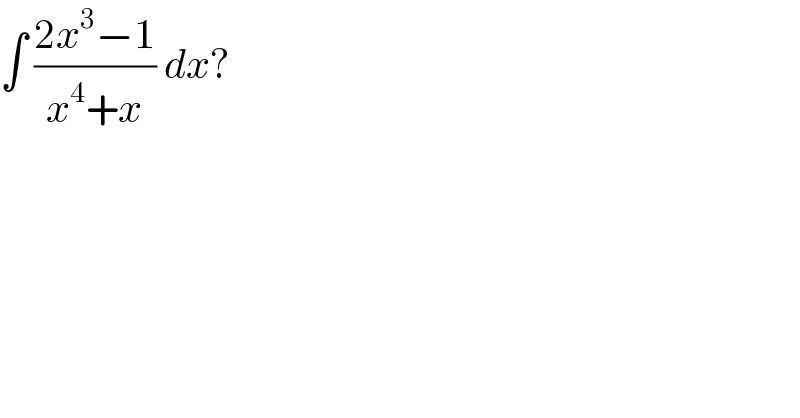
∫ ((2x^3 −1)/(x^4 +x)) dx?
$$\int\:\frac{\mathrm{2}{x}^{\mathrm{3}} −\mathrm{1}}{{x}^{\mathrm{4}} +{x}}\:{dx}? \\ $$
Commented by john santu last updated on 12/Jan/20
we divide by x^2 ∫ ((2x−(1/x^2 ))/(x^2 +(1/x))) dx now by using integration substitution “u“ let u = x^2 +(1/x) ⇒ du = 2x−(1/x^2 ) dx ∫ (du/u) = ln ∣u∣+c = ln ∣x^2 +(1/x)∣+c
$${we}\:{divide}\:{by}\:{x}^{\mathrm{2}} \\ $$$$\int\:\frac{\mathrm{2}{x}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}}\:{dx} \\ $$$${now}\:{by}\:{using}\:{integration}\: \\ $$$${substitution}\:“{u}“\: \\ $$$${let}\:{u}\:=\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}\:\Rightarrow\:{du}\:=\:\mathrm{2}{x}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{dx} \\ $$$$\int\:\frac{{du}}{{u}}\:=\:{ln}\:\mid{u}\mid+{c}\:=\:{ln}\:\mid{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}}\mid+{c} \\ $$
Commented by jagoll last updated on 12/Jan/20
thank you
$${thank}\:{you} \\ $$
Commented by mathmax by abdo last updated on 13/Jan/20
let decompose F(x)=((2x^3 −1)/(x^4 +x)) ⇒F(x)=((2x^3 −1)/(x(x^3 +1))) =((2x^3 −1)/(x(x+1)(x^2 −x+1))) =(a/x) +(b/(x+1)) +((cx+d)/(x^2 −x+1)) a =xF(x)∣_(x=0) =−1 b=(x+1)F(x)∣_(x=−1) =((−3)/(−3))=1 ⇒F(x)=−(1/x)+(1/(x+1)) +((cx+d)/(x^2 −x+1)) lim_(x→+∞) xF(x)=2=c ⇒F(x)=−(1/x)+(1/(x+1)) +((2x+d)/(x^2 −x+1)) F(1)=(1/2) =−1+(1/2) +2+d ⇒d=−1 ⇒ F(x)=−(1/x)+(1/(x+1)) +((2x−1)/(x^2 −x+1)) ⇒∫F(x)dx=−ln∣x∣+ln∣x+1∣+ln(x^2 −x+1)+c =ln∣x^3 +1∣−ln∣x∣ +c =ln∣((x^3 +1)/x)∣ +C =ln∣x^2 +(1/x)∣ +C
$${let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{2}{x}^{\mathrm{3}} −\mathrm{1}}{{x}^{\mathrm{4}} \:+{x}}\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{2}{x}^{\mathrm{3}} −\mathrm{1}}{{x}\left({x}^{\mathrm{3}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{3}} −\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}\:=\frac{{a}}{{x}}\:+\frac{{b}}{{x}+\mathrm{1}}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${a}\:={xF}\left({x}\right)\mid_{{x}=\mathrm{0}} \:=−\mathrm{1} \\ $$$${b}=\left({x}+\mathrm{1}\right){F}\left({x}\right)\mid_{{x}=−\mathrm{1}} =\frac{−\mathrm{3}}{−\mathrm{3}}=\mathrm{1}\:\Rightarrow{F}\left({x}\right)=−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{2}={c}\:\Rightarrow{F}\left({x}\right)=−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{\mathrm{2}{x}+{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:=−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{2}+{d}\:\Rightarrow{d}=−\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)=−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:\Rightarrow\int{F}\left({x}\right){dx}=−{ln}\mid{x}\mid+{ln}\mid{x}+\mathrm{1}\mid+{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+{c} \\ $$$$ \\ $$$$={ln}\mid{x}^{\mathrm{3}} +\mathrm{1}\mid−{ln}\mid{x}\mid\:+{c}\:\:={ln}\mid\frac{{x}^{\mathrm{3}} +\mathrm{1}}{{x}}\mid\:+{C} \\ $$$$={ln}\mid{x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{x}}\mid\:+{C} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *