Question Number 137938 by Ñï= last updated on 09/Apr/21
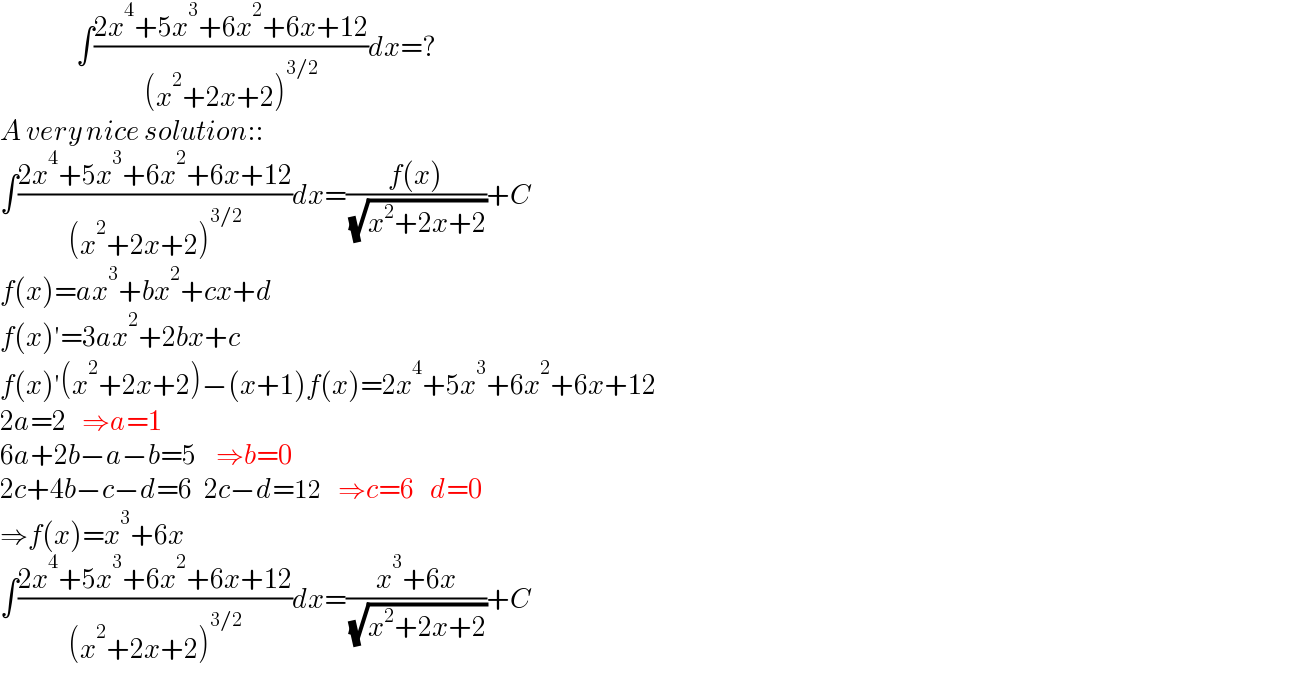
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\frac{\mathrm{2}{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{12}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{3}/\mathrm{2}} }{dx}=? \\ $$$${A}\:{very}\:{nice}\:{solution}:: \\ $$$$\int\frac{\mathrm{2}{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{12}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{3}/\mathrm{2}} }{dx}=\frac{{f}\left({x}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}}+{C} \\ $$$${f}\left({x}\right)={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${f}\left({x}\right)'=\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c} \\ $$$${f}\left({x}\right)'\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)−\left({x}+\mathrm{1}\right){f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{12} \\ $$$$\mathrm{2}{a}=\mathrm{2}\:\:\:\:\Rightarrow{a}=\mathrm{1} \\ $$$$\mathrm{6}{a}+\mathrm{2}{b}−{a}−{b}=\mathrm{5}\:\:\:\:\:\Rightarrow{b}=\mathrm{0} \\ $$$$\mathrm{2}{c}+\mathrm{4}{b}−{c}−{d}=\mathrm{6}\:\:\:\mathrm{2}{c}−{d}=\mathrm{12}\:\:\:\:\Rightarrow{c}=\mathrm{6}\:\:\:\:{d}=\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)={x}^{\mathrm{3}} +\mathrm{6}{x} \\ $$$$\int\frac{\mathrm{2}{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{12}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{3}/\mathrm{2}} }{dx}=\frac{{x}^{\mathrm{3}} +\mathrm{6}{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}}+{C} \\ $$
Commented by SLVR last updated on 11/Apr/21
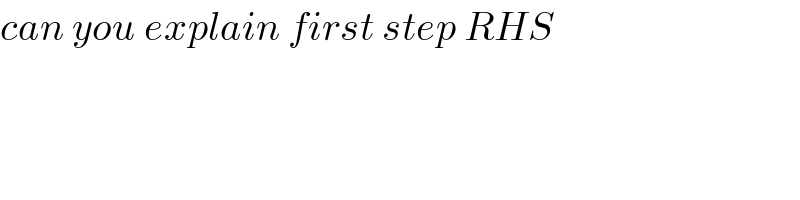
$${can}\:{you}\:{explain}\:{first}\:{step}\:{RHS} \\ $$
