Question Number 6016 by sanusihammed last updated on 09/Jun/16
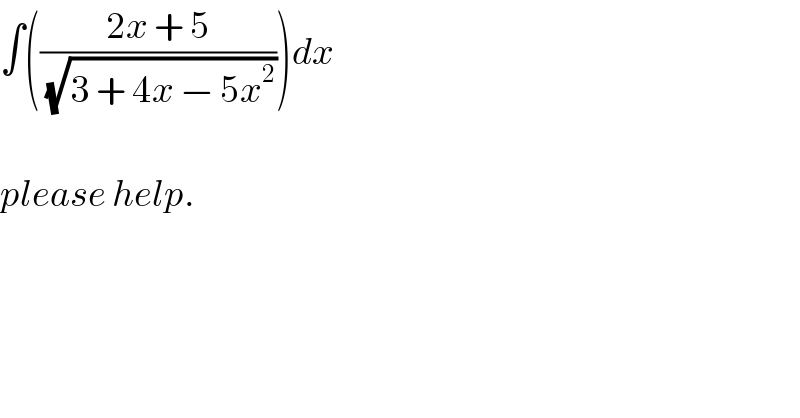
$$\int\left(\frac{\mathrm{2}{x}\:+\:\mathrm{5}}{\:\sqrt{\mathrm{3}\:+\:\mathrm{4}{x}\:−\:\mathrm{5}{x}^{\mathrm{2}} }}\right){dx} \\ $$$$ \\ $$$${please}\:{help}. \\ $$
Answered by Yozzii last updated on 09/Jun/16

$${Let}\:{u}=\mathrm{3}+\mathrm{4}{x}−\mathrm{5}{x}^{\mathrm{2}} \Rightarrow{du}=\left(\mathrm{4}−\mathrm{10}{x}\right){dx} \\ $$$$−{du}=\left(\mathrm{10}{x}−\mathrm{4}\right){dx} \\ $$$${u}=\mathrm{3}−\mathrm{5}\left({x}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{5}}{x}+\left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{2}} \right) \\ $$$${u}=\mathrm{3}−\mathrm{5}\left(\left({x}−\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{25}}\right) \\ $$$${u}=\frac{\mathrm{95}}{\mathrm{25}}−\mathrm{5}\left({x}−\mathrm{0}.\mathrm{4}\right)^{\mathrm{2}} =\mathrm{5}\left(\frac{\mathrm{95}}{\mathrm{125}}−\left({x}−\mathrm{0}.\mathrm{4}\right)^{\mathrm{2}} \right) \\ $$$$\sqrt{{u}}=\sqrt{\mathrm{5}}\sqrt{\frac{\mathrm{19}}{\mathrm{25}}−\left({x}−\mathrm{0}.\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${I}=\int\frac{\mathrm{2}{x}+\mathrm{5}}{\:\sqrt{{u}}}{dx}=−\int\frac{−\mathrm{5}−\mathrm{2}{x}}{\:\sqrt{{u}}}{dx}=−\int\frac{\mathrm{0}.\mathrm{2}\left(\mathrm{4}−\mathrm{29}−\mathrm{10}{x}\right)}{\:\sqrt{{u}}}{dx} \\ $$$$\int\frac{−\mathrm{0}.\mathrm{2}\left(−\mathrm{29}\right)−\mathrm{0}.\mathrm{2}\left(\mathrm{4}−\mathrm{10}{x}\right)}{\:\sqrt{{u}}}{dx}=\int\frac{\mathrm{29}}{\mathrm{5}\sqrt{{u}}}{dx}−\int\frac{\mathrm{4}−\mathrm{10}{x}}{\mathrm{5}\sqrt{{u}}}{dx}=\int\frac{\mathrm{29}}{\mathrm{5}\sqrt{{u}}}{dx}−\int\frac{\frac{{du}}{{dx}}}{\mathrm{5}\sqrt{{u}}}{dx} \\ $$$${I}=\frac{\mathrm{29}}{\mathrm{5}}\int\frac{{dx}}{\:\sqrt{{u}}}−\frac{\mathrm{1}}{\mathrm{5}}\int{u}^{−\mathrm{0}.\mathrm{5}} {du} \\ $$$${I}=\frac{\mathrm{29}}{\mathrm{5}\sqrt{\mathrm{5}}}\int\frac{{dx}}{\:\sqrt{\frac{\mathrm{19}}{\mathrm{25}}−\left({x}−\mathrm{0}.\mathrm{4}\right)^{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{2}{u}^{\mathrm{0}.\mathrm{5}} \\ $$$${I}=\frac{\mathrm{29}}{\mathrm{5}\sqrt{\mathrm{5}}}{sin}^{−\mathrm{1}} \frac{\mathrm{5}{x}−\mathrm{2}}{\:\sqrt{\mathrm{19}}}−\frac{\mathrm{2}}{\mathrm{5}}\sqrt{\mathrm{3}+\mathrm{4}{x}−\mathrm{5}{x}^{\mathrm{2}} }+{C} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by sanusihammed last updated on 09/Jun/16

$${Thanks}\:{so}\:{much} \\ $$
