Question Number 69894 by Rio Michael last updated on 28/Sep/19
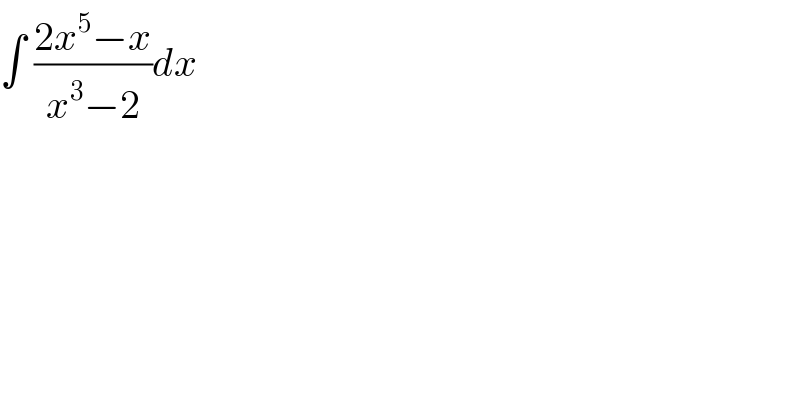
$$\int\:\frac{\mathrm{2}{x}^{\mathrm{5}} −{x}}{{x}^{\mathrm{3}} −\mathrm{2}}{dx} \\ $$
Commented by abdo mathsup 649 cc last updated on 29/Sep/19

$${I}=\int\:\:\frac{\mathrm{2}{x}^{\mathrm{5}} −{x}}{{x}^{\mathrm{3}} −\mathrm{2}}{dx}\:=\int\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} \left({x}^{\mathrm{3}} −\mathrm{2}\right)+\mathrm{4}{x}^{\mathrm{2}} −{x}}{{x}^{\mathrm{3}} −\mathrm{2}}{dx} \\ $$$$=\int\:\:\mathrm{2}{x}^{\mathrm{2}} {dx}\:+\int\:\:\frac{\mathrm{4}{x}^{\mathrm{2}} −{x}}{{x}^{\mathrm{3}} −\mathrm{2}}{dx} \\ $$$$\int\:\mathrm{2}{x}^{\mathrm{2}\:} \:=\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}\:} \:+{c}\:\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\frac{\mathrm{4}{x}^{\mathrm{2}} −{x}}{{x}^{\mathrm{3}} −\mathrm{2}}\:\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{4}{x}^{\mathrm{2}} −{x}}{\left({x}−\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)\left({x}^{\mathrm{2}} +{x}\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)+\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)^{\mathrm{2}} \right)\right.} \\ $$$${let}\:{put}\:^{\mathrm{3}} \sqrt{\mathrm{2}}=\alpha\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{4}{x}^{\mathrm{2}} −{x}}{\left({x}−\alpha\right)\left({x}^{\mathrm{2}} +\alpha{x}\:+\alpha^{\mathrm{2}} \right)} \\ $$$$=\frac{{a}}{{x}−\alpha}\:+\frac{{bx}\:+{c}}{{x}^{\mathrm{2}} +\alpha{x}\:+\alpha^{\mathrm{2}} } \\ $$$${a}\:=\frac{\mathrm{4}\alpha^{\mathrm{2}} −\alpha}{\mathrm{3}\alpha^{\mathrm{2}} }\:=\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{3}\alpha}=\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}\alpha} \\ $$$${lim}_{{x}−\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{4}\:={a}+{b}\:\Rightarrow{b}=\mathrm{4}−{a} \\ $$$$=\mathrm{4}−\left(\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}\alpha}\right)=\frac{\mathrm{8}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{3}\alpha} \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{0}=−\frac{{a}}{\alpha}\:+\frac{{c}}{\alpha^{\mathrm{2}} }\:=\frac{{c}−\alpha{a}}{\alpha^{\mathrm{2}} }\:\Rightarrow{c}=\alpha{a}=\frac{\mathrm{4}\alpha}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\int\:\:{F}\left({x}\right){dx}\:={aln}\mid{x}−\alpha\mid\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2}{bx}+\mathrm{2}{c}}{{x}^{\mathrm{2}} \:+\alpha{x}\:+\alpha^{\mathrm{2}} }{dx} \\ $$$$={aln}\mid{x}−\alpha\mid+\frac{{b}}{\mathrm{2}}\:\int\:\:\frac{\mathrm{2}{x}+\alpha−\alpha\:+\mathrm{2}{c}}{{x}^{\mathrm{2}} \:+\alpha{x}\:+\alpha^{\mathrm{2}} }{dx} \\ $$$$={aln}\mid{x}−\alpha\mid\:+\frac{{b}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+\alpha{x}\:+\alpha^{\mathrm{2}} \right)+\frac{\left(\mathrm{2}{c}−\alpha\right){b}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} \:+\alpha{x}\:+\alpha^{\mathrm{2}} } \\ $$$${and}\:\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\alpha{x}+\alpha^{\mathrm{2}} }=\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}\frac{\alpha}{\mathrm{2}}{x}\:+\frac{\alpha^{\mathrm{2}} }{\mathrm{4}}+\alpha^{\mathrm{2}} −\frac{\alpha^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$=\int\:\:\frac{{dx}}{\left({x}+\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}\alpha^{\mathrm{2}} }{\mathrm{4}}}\:=_{{x}+\frac{\alpha}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}\alpha^{\mathrm{2}} }\:\int\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\alpha^{\mathrm{2}} }{arctan}\left(\frac{\mathrm{2}{x}+\alpha}{\:\sqrt{\mathrm{3}}}\right)\:+{c}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} \:+{aln}\mid{x}−\alpha\mid+\frac{{b}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+\alpha{x}\:+\alpha^{\mathrm{2}} \right) \\ $$$$+\frac{\left(\mathrm{2}{c}−\alpha\right){b}}{\:\sqrt{\mathrm{3}}\alpha^{\mathrm{2}} }\:{arctan}\left(\frac{\mathrm{2}{x}+\alpha}{\:\sqrt{\mathrm{3}}}\right)\:+{C}\:\:{with}\:\alpha=^{\mathrm{3}} \sqrt{\mathrm{2}} \\ $$
Commented by Rio Michael last updated on 29/Sep/19

$${thanks}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 29/Sep/19
$${you}\:{are}\:{welcome}. \\ $$
