Question Number 142538 by Rankut last updated on 02/Jun/21

$$\mathrm{2}\boldsymbol{{x}}^{\mathrm{7}} +\boldsymbol{{x}}^{\mathrm{28}} =\mathrm{3}\boldsymbol{{x}}^{\mathrm{21}} \\ $$$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{x}} \\ $$
Answered by Ar Brandon last updated on 02/Jun/21
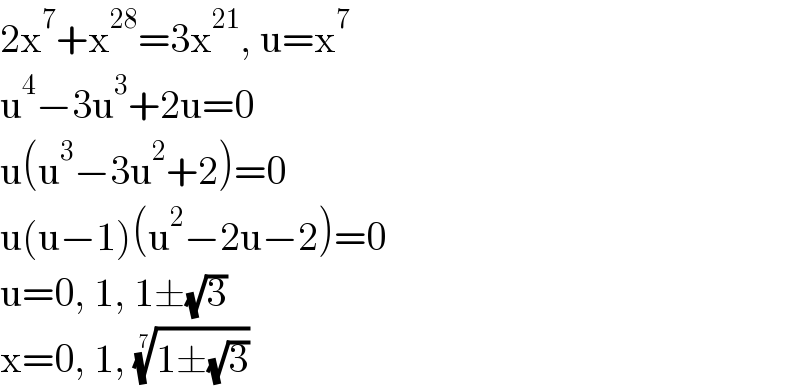
$$\mathrm{2x}^{\mathrm{7}} +\mathrm{x}^{\mathrm{28}} =\mathrm{3x}^{\mathrm{21}} ,\:\mathrm{u}=\mathrm{x}^{\mathrm{7}} \\ $$$$\mathrm{u}^{\mathrm{4}} −\mathrm{3u}^{\mathrm{3}} +\mathrm{2u}=\mathrm{0} \\ $$$$\mathrm{u}\left(\mathrm{u}^{\mathrm{3}} −\mathrm{3u}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{u}\left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{u}^{\mathrm{2}} −\mathrm{2u}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{u}=\mathrm{0},\:\mathrm{1},\:\mathrm{1}\pm\sqrt{\mathrm{3}} \\ $$$$\mathrm{x}=\mathrm{0},\:\mathrm{1},\:\sqrt[{\mathrm{7}}]{\mathrm{1}\pm\sqrt{\mathrm{3}}} \\ $$
Commented by MJS_new last updated on 02/Jun/21

$$\mathrm{we}\:\mathrm{must}\:\mathrm{find}\:\mathrm{28}\:\mathrm{solutions} \\ $$
Commented by Ar Brandon last updated on 02/Jun/21

$$\mathrm{in}\:\mathbb{R}\:? \\ $$
Commented by JDamian last updated on 02/Jun/21
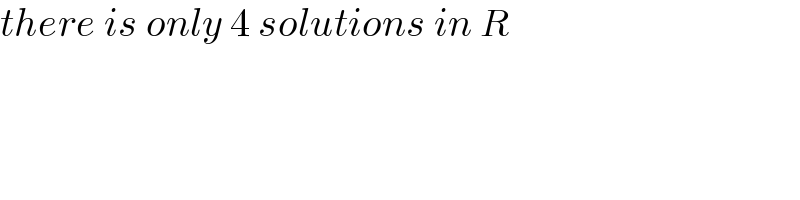
$${there}\:{is}\:{only}\:\mathrm{4}\:{solutions}\:{in}\:{R} \\ $$
Commented by MJS_new last updated on 02/Jun/21
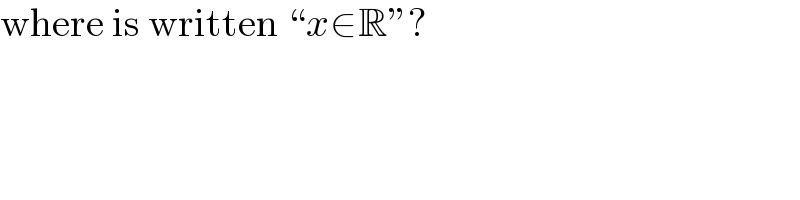
$$\mathrm{where}\:\mathrm{is}\:\mathrm{written}\:“{x}\in\mathbb{R}''? \\ $$
