Question Number 71141 by Mr. K last updated on 12/Oct/19

$$\left(\mathrm{2}{x}\right)^{{x}} =\frac{\mathrm{1}}{\mathrm{16}} \\ $$
Commented by mr W last updated on 12/Oct/19

$$\left(\mathrm{2}{x}\right)^{{x}} =\sqrt{\left(\mathrm{2}{x}\right)^{\mathrm{2}{x}} }=\sqrt{{t}^{{t}} }\geqslant\sqrt{{e}^{−\frac{\mathrm{1}}{{e}}} }=\mathrm{0}.\mathrm{832}>\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\Rightarrow{no}\:{real}\:{solution}\:{for}\:\left(\mathrm{2}{x}\right)^{{x}} =\frac{\mathrm{1}}{\mathrm{16}} \\ $$
Commented by Henri Boucatchou last updated on 12/Oct/19

$$\boldsymbol{{Correct}}\:\:\boldsymbol{{Sir}},\:\:\boldsymbol{{no}}\:\:\boldsymbol{{real}}\:\:\boldsymbol{{solution}},\:{the}\:\:{geometric}\:\:{prof}\:\:{also}\:\:{show}\:\:{it} \\ $$
Commented by mr W last updated on 12/Oct/19
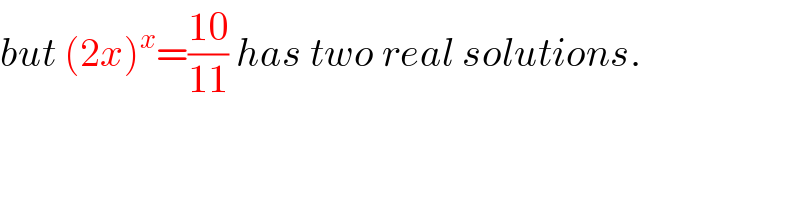
$${but}\:\left(\mathrm{2}{x}\right)^{{x}} =\frac{\mathrm{10}}{\mathrm{11}}\:{has}\:{two}\:{real}\:{solutions}. \\ $$
Commented by mr W last updated on 13/Oct/19

$$\left(\mathrm{2}{x}\right)^{{x}} =\frac{\mathrm{1}}{\mathrm{16}}\:{has}\:{no}\:{real}\:{solution}. \\ $$$${let}'{s}\:{say}\:{the}\:{question}\:{were}\:\left(\mathrm{2}{x}\right)^{{x}} ={a}=\frac{\mathrm{10}}{\mathrm{11}} \\ $$$$\left(\mathrm{2}{x}\right)^{{x}} ={a} \\ $$$$\mathrm{2}{x}={a}^{\frac{\mathrm{1}}{{x}}} ={e}^{\frac{\mathrm{ln}\:{a}}{{x}}} \\ $$$$\mathrm{2ln}\:{a}=\frac{\mathrm{ln}\:{a}}{{x}}{e}^{\frac{\mathrm{ln}\:{a}}{{x}}} \\ $$$$\Rightarrow\frac{\mathrm{ln}\:{a}}{{x}}={W}\left(\mathrm{2ln}\:{a}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{ln}\:{a}}{{W}\left(\mathrm{2ln}\:{a}\right)} \\ $$$${such}\:{that}\:{real}\:{solution}\:{exists}, \\ $$$$\mathrm{2ln}\:{a}\geqslant−\frac{\mathrm{1}}{{e}}\:\Rightarrow{a}\geqslant\frac{\mathrm{1}}{{e}^{\frac{\mathrm{1}}{\mathrm{2}{e}}} }=\mathrm{0}.\mathrm{832} \\ $$$${with}\:{a}=\frac{\mathrm{10}}{\mathrm{11}}\:{which}\:{is}\:>\mathrm{0}.\mathrm{832} \\ $$$$\Rightarrow{x}=\frac{\mathrm{ln}\:\frac{\mathrm{10}}{\mathrm{11}}}{{W}\left(\mathrm{2ln}\:\frac{\mathrm{10}}{\mathrm{11}}\right)}=\begin{cases}{\frac{\mathrm{ln}\:\mathrm{10}−\mathrm{ln}\:\mathrm{11}}{−\mathrm{0}.\mathrm{243071}}=\mathrm{0}.\mathrm{392108}}\\{\frac{\mathrm{ln}\:\mathrm{10}−\mathrm{ln}\:\mathrm{11}}{−\mathrm{2}.\mathrm{621044}}=\mathrm{0}.\mathrm{036363}}\end{cases} \\ $$
Commented by Mr. K last updated on 13/Oct/19

$${Can}\:{you}\:{show}\:{the}\:{solution}? \\ $$
Commented by Mr. K last updated on 13/Oct/19

$${thank}\:{you}. \\ $$
