Question Number 72569 by otchereabdullai@gmail.com last updated on 30/Oct/19
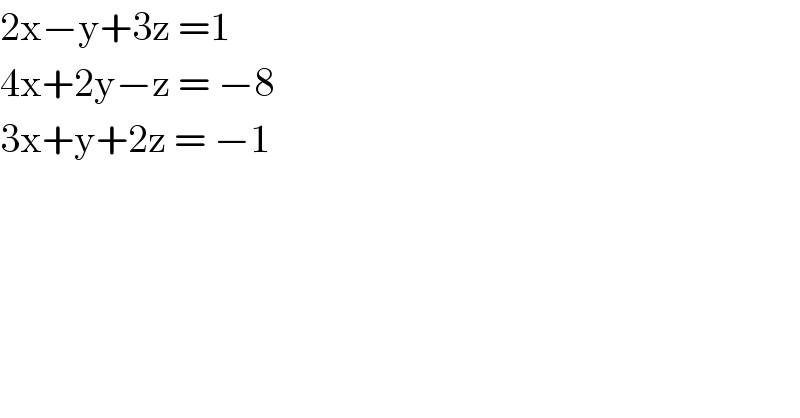
$$\mathrm{2x}−\mathrm{y}+\mathrm{3z}\:=\mathrm{1} \\ $$$$\mathrm{4x}+\mathrm{2y}−\mathrm{z}\:=\:−\mathrm{8} \\ $$$$\mathrm{3x}+\mathrm{y}+\mathrm{2z}\:=\:−\mathrm{1} \\ $$
Answered by MJS last updated on 30/Oct/19

$$\left(\mathrm{2}\right)\:\:{z}=\mathrm{4}{x}+\mathrm{2}{y}+\mathrm{8} \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{14}{x}+\mathrm{5}{y}+\mathrm{23}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:\mathrm{11}{x}+\mathrm{5}{y}+\mathrm{17}=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{3}\right)\:\:\mathrm{3}{x}+\mathrm{6}=\mathrm{0}\:\Rightarrow\:{x}=−\mathrm{2} \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{5}{y}−\mathrm{5}=\mathrm{0}\:\Rightarrow\:{y}=\mathrm{1} \\ $$$$\Rightarrow\:{z}=\mathrm{2} \\ $$
Commented by otchereabdullai@gmail.com last updated on 30/Oct/19

$$\mathrm{thanks}\:\mathrm{prof}\:\mathrm{mjs} \\ $$
Answered by Tanmay chaudhury last updated on 30/Oct/19

$$\bigtriangleup=\mid\mathrm{2}\:−\mathrm{1}\:\:\:\:\:\mathrm{3}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\mid\mathrm{4}\:\:\:\:\mathrm{2}\:\:\:−\mathrm{1}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\mid\mathrm{3}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{2}\mid=\mathrm{2}\left(\mathrm{4}+\mathrm{1}\right)+\mathrm{1}\left(\mathrm{8}+\mathrm{3}\right)+\mathrm{3}\left(\mathrm{4}−\mathrm{6}\right) \\ $$$$\:\:\:\bigtriangleup=\mathrm{15} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{15}}×\:\:\mid\mathrm{1}\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{3}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid−\mathrm{8}\:\:\:\:\:\mathrm{2}\:\:\:\:\:−\mathrm{1}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid−\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{2}\mid \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{15}}×\left\{\mathrm{1}\left(\mathrm{4}+\mathrm{1}\right)+\mathrm{1}\left(−\mathrm{16}−\mathrm{1}\right)+\mathrm{3}\left(−\mathrm{8}+\mathrm{2}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{15}}×\left\{\mathrm{5}−\mathrm{17}−\mathrm{18}\right\}=−\mathrm{2} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{15}}×\mid\:\mathrm{2}\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\mathrm{4}\:\:\:\:−\mathrm{8}\:\:\:−\mathrm{1}\mid=\mathrm{2}\left(−\mathrm{16}−\mathrm{1}\right)−\mathrm{1}\left(\mathrm{8}+\mathrm{3}\right)+\mathrm{3}\left(−\mathrm{4}+\mathrm{24}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\mathrm{3}\:\:\:\:−\mathrm{1}\:\:\:\:\:\mathrm{2}\:\:\:\mid=−\mathrm{34}−\mathrm{11}+\mathrm{60}=\mathrm{15} \\ $$$${so}\:{y}=\frac{\mathrm{15}}{\mathrm{15}}=\mathrm{1} \\ $$$$\mathrm{2}{x}−{y}+\mathrm{3}{z}=\mathrm{1} \\ $$$$\mathrm{2}×−\mathrm{2}−\mathrm{1}+\mathrm{3}{z}=\mathrm{1} \\ $$$$\mathrm{3}{z}=\mathrm{1}+\mathrm{5}\rightarrow{z}=\mathrm{2} \\ $$$$\boldsymbol{{x}}=−\mathrm{2}\:\:\:\boldsymbol{{y}}=\mathrm{1}\:\:\:\boldsymbol{{z}}=\mathrm{2} \\ $$
Commented by otchereabdullai@gmail.com last updated on 30/Oct/19

$$\mathrm{thanks}\:\mathrm{prof}\:\mathrm{tanmay} \\ $$
Answered by malwaan last updated on 30/Oct/19

$$\left(\mathrm{1}\right)+\left(\mathrm{3}\right)\:\mathrm{5}\boldsymbol{{x}}\:+\:\mathrm{5}\boldsymbol{{z}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{x}}\:=\:−\boldsymbol{{z}}\:;\:\boldsymbol{{z}}\:=\:−\boldsymbol{{x}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{5}\boldsymbol{{x}}+\mathrm{2}\boldsymbol{{y}}\:=\:−\mathrm{8}\rightarrow\ast \\ $$$$\left(\mathrm{3}\right)\:\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\:=\:−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{2}\boldsymbol{{x}}+\mathrm{2}\boldsymbol{{y}}=−\mathrm{2} \\ $$$$\left(\ast\right)\:\mathrm{3}\boldsymbol{{x}}\:=\:−\mathrm{6}\:\therefore\:\boldsymbol{{x}}\:=\:−\mathrm{2}\:;\:\boldsymbol{{z}}=\mathrm{2} \\ $$$$;\:\boldsymbol{{y}}=\mathrm{2}−\mathrm{1}=\mathrm{1} \\ $$
