Question Number 139861 by mathdanisur last updated on 01/May/21
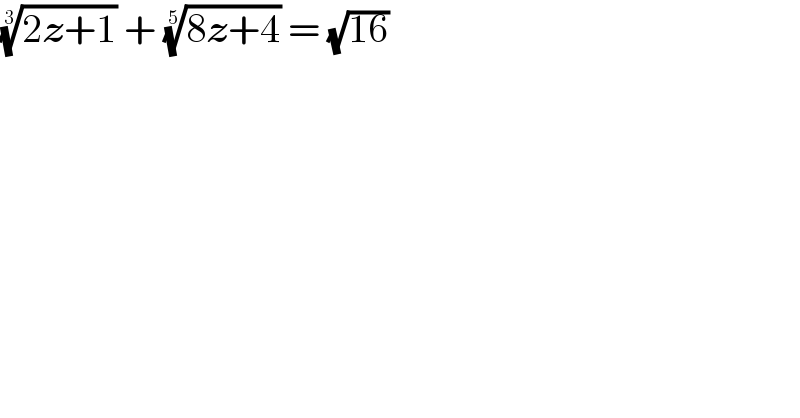
$$\sqrt[{\mathrm{3}}]{\mathrm{2}\boldsymbol{{z}}+\mathrm{1}}\:+\:\sqrt[{\mathrm{5}}]{\mathrm{8}\boldsymbol{{z}}+\mathrm{4}}\:=\:\sqrt{\mathrm{16}} \\ $$
Answered by mindispower last updated on 01/May/21

$${z}=\frac{\mathrm{7}}{\mathrm{2}},{solution} \\ $$$${over}\:\mathbb{R} \\ $$$${f}\left({z}\right)=\sqrt[{\mathrm{3}}]{\mathrm{2}{z}+\mathrm{1}}+\sqrt[{\mathrm{5}}]{\mathrm{8}{z}+\mathrm{4}}\:{is}\:{increase}\:{function} \\ $$$$\underset{{z}\rightarrow−\infty} {\mathrm{lim}}{f}\left({z}\right)=−\infty \\ $$$$\underset{{z}\rightarrow+\infty} {\mathrm{lim}}{f}\left({z}\right)=+\infty,{f}\left(\frac{\mathrm{7}}{\mathrm{2}}\right)=\mathrm{4} \\ $$$${S}=\left\{\frac{\mathrm{7}}{\mathrm{2}}\right\} \\ $$$$ \\ $$$$ \\ $$
Commented by mathdanisur last updated on 02/May/21

$${thanks}\:{sir} \\ $$
Answered by MJS_new last updated on 02/May/21
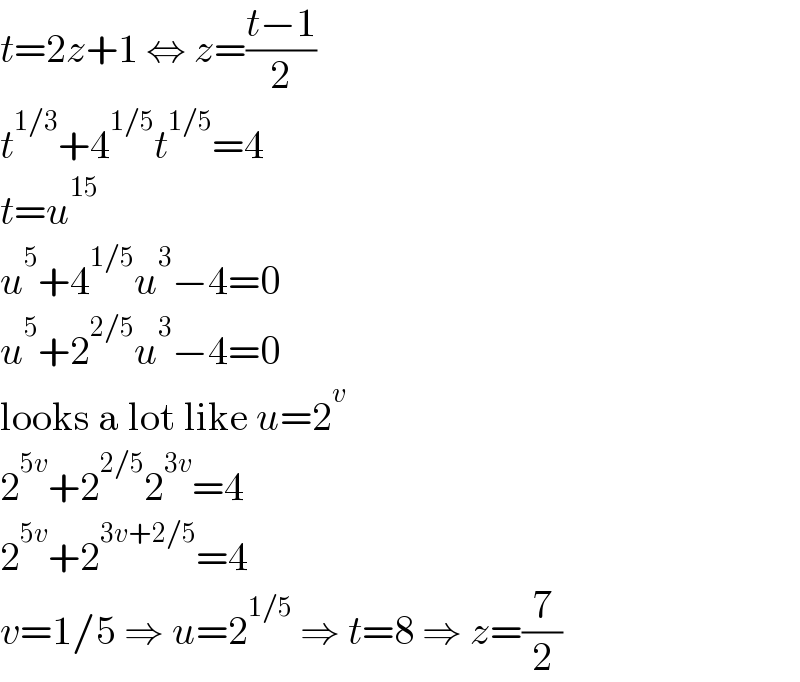
$${t}=\mathrm{2}{z}+\mathrm{1}\:\Leftrightarrow\:{z}=\frac{{t}−\mathrm{1}}{\mathrm{2}} \\ $$$${t}^{\mathrm{1}/\mathrm{3}} +\mathrm{4}^{\mathrm{1}/\mathrm{5}} {t}^{\mathrm{1}/\mathrm{5}} =\mathrm{4} \\ $$$${t}={u}^{\mathrm{15}} \\ $$$${u}^{\mathrm{5}} +\mathrm{4}^{\mathrm{1}/\mathrm{5}} {u}^{\mathrm{3}} −\mathrm{4}=\mathrm{0} \\ $$$${u}^{\mathrm{5}} +\mathrm{2}^{\mathrm{2}/\mathrm{5}} {u}^{\mathrm{3}} −\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{looks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{like}\:{u}=\mathrm{2}^{{v}} \\ $$$$\mathrm{2}^{\mathrm{5}{v}} +\mathrm{2}^{\mathrm{2}/\mathrm{5}} \mathrm{2}^{\mathrm{3}{v}} =\mathrm{4} \\ $$$$\mathrm{2}^{\mathrm{5}{v}} +\mathrm{2}^{\mathrm{3}{v}+\mathrm{2}/\mathrm{5}} =\mathrm{4} \\ $$$${v}=\mathrm{1}/\mathrm{5}\:\Rightarrow\:{u}=\mathrm{2}^{\mathrm{1}/\mathrm{5}} \:\Rightarrow\:{t}=\mathrm{8}\:\Rightarrow\:{z}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 02/May/21

$${thankyou}\:{sir} \\ $$
