Question Number 10855 by Joel576 last updated on 27/Feb/17
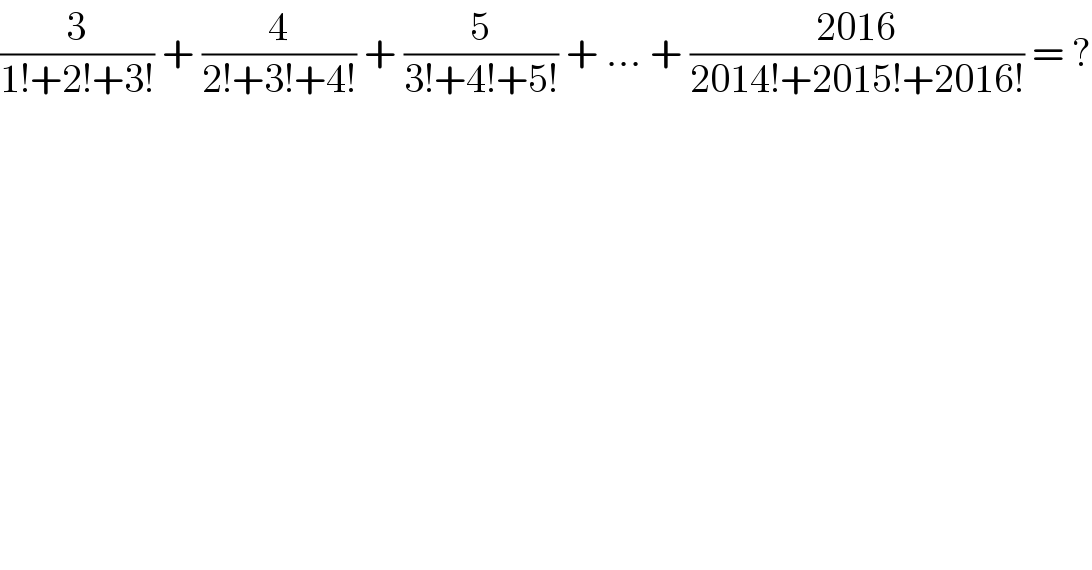
$$\frac{\mathrm{3}}{\mathrm{1}!+\mathrm{2}!+\mathrm{3}!}\:+\:\frac{\mathrm{4}}{\mathrm{2}!+\mathrm{3}!+\mathrm{4}!}\:+\:\frac{\mathrm{5}}{\mathrm{3}!+\mathrm{4}!+\mathrm{5}!}\:+\:…\:+\:\frac{\mathrm{2016}}{\mathrm{2014}!+\mathrm{2015}!+\mathrm{2016}!}\:=\:? \\ $$
Answered by nume1114 last updated on 28/Feb/17
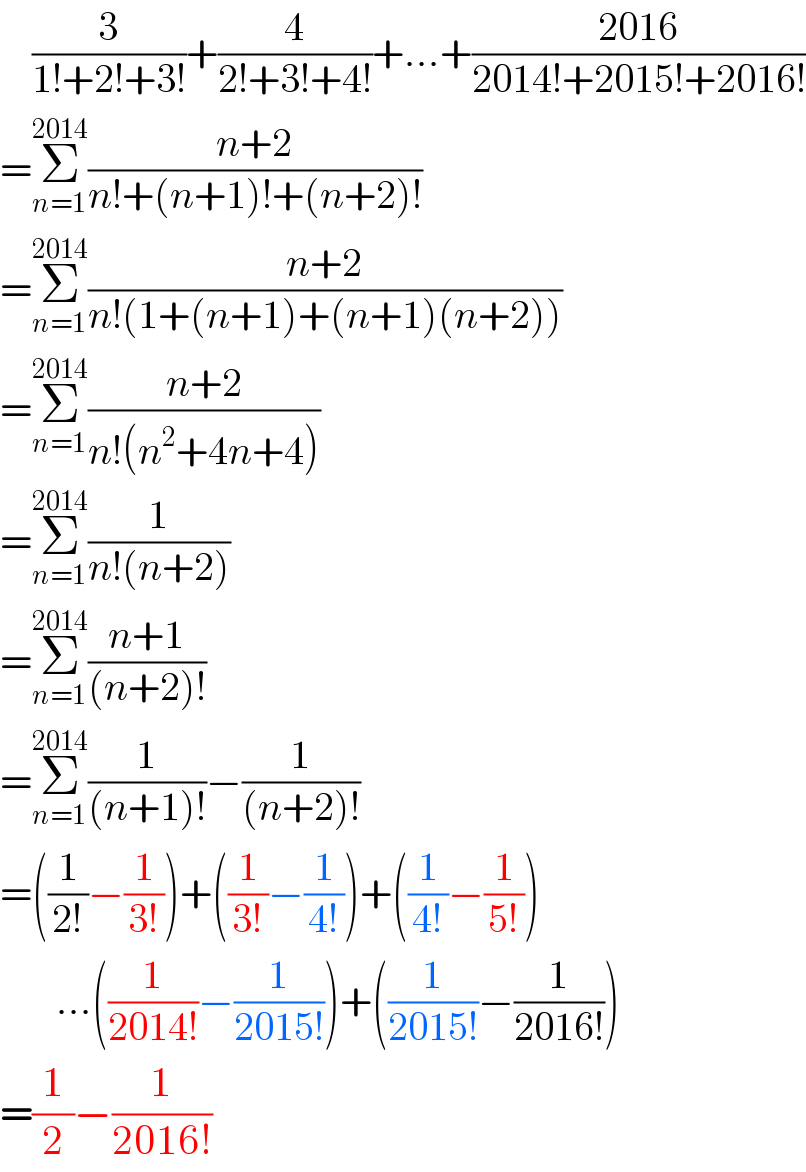
$$\:\:\:\:\frac{\mathrm{3}}{\mathrm{1}!+\mathrm{2}!+\mathrm{3}!}+\frac{\mathrm{4}}{\mathrm{2}!+\mathrm{3}!+\mathrm{4}!}+…+\frac{\mathrm{2016}}{\mathrm{2014}!+\mathrm{2015}!+\mathrm{2016}!} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2014}} {\sum}}\frac{{n}+\mathrm{2}}{{n}!+\left({n}+\mathrm{1}\right)!+\left({n}+\mathrm{2}\right)!} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2014}} {\sum}}\frac{{n}+\mathrm{2}}{{n}!\left(\mathrm{1}+\left({n}+\mathrm{1}\right)+\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\right)} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2014}} {\sum}}\frac{{n}+\mathrm{2}}{{n}!\left({n}^{\mathrm{2}} +\mathrm{4}{n}+\mathrm{4}\right)} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2014}} {\sum}}\frac{\mathrm{1}}{{n}!\left({n}+\mathrm{2}\right)} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2014}} {\sum}}\frac{{n}+\mathrm{1}}{\left({n}+\mathrm{2}\right)!} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2014}} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)!} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{4}!}−\frac{\mathrm{1}}{\mathrm{5}!}\right) \\ $$$$\:\:\:\:\:\:\:…\left(\frac{\mathrm{1}}{\mathrm{2014}!}−\frac{\mathrm{1}}{\mathrm{2015}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{2015}!}−\frac{\mathrm{1}}{\mathrm{2016}!}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2016}!} \\ $$
Commented by Joel576 last updated on 01/Mar/17
$${thank}\:{you}\:{very}\:{much} \\ $$
