Menu Close

3-2-2-1-2-4-1-2-8-1-2-16-1-2-32-1-2-64-1-2-128-1-

Tinku Tara 0 Comments
Pin




Question Number 10575 by ridwan balatif last updated on 19/Feb/17
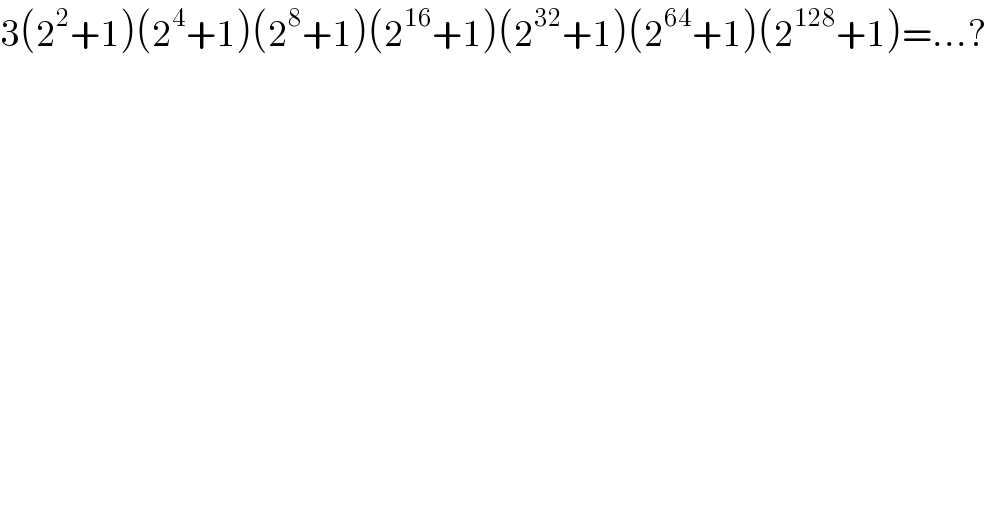
3(2^2 +1)(2^4 +1)(2^8 +1)(2^(16) +1)(2^(32) +1)(2^(64) +1)(2^(128) +1)=...?
$$\mathrm{3}\left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{4}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{8}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{16}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{32}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{64}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right)=…? \\ $$
Commented by FilupS last updated on 19/Feb/17
3=(2^1 +1) S=Π_(i=1) ^8 (2^((2^(n−1) )) +1)
$$\mathrm{3}=\left(\mathrm{2}^{\mathrm{1}} +\mathrm{1}\right) \\ $$$${S}=\underset{{i}=\mathrm{1}} {\overset{\mathrm{8}} {\prod}}\left(\mathrm{2}^{\left(\mathrm{2}^{{n}−\mathrm{1}} \right)} +\mathrm{1}\right) \\ $$
Answered by prakash jain last updated on 19/Feb/17
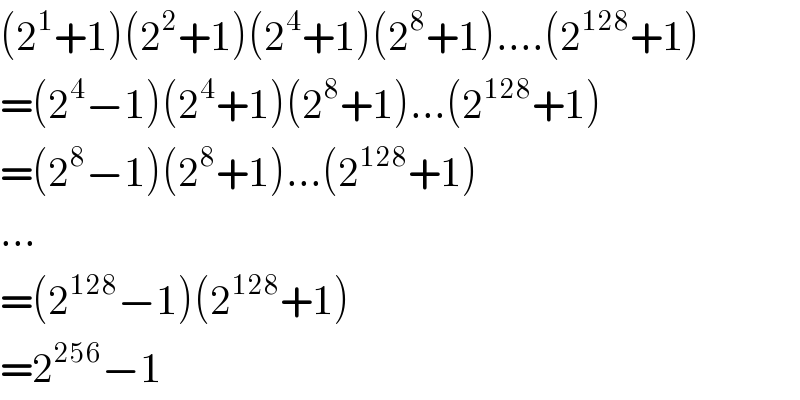
(2^1 +1)(2^2 +1)(2^4 +1)(2^8 +1)....(2^(128) +1) =(2^4 −1)(2^4 +1)(2^8 +1)...(2^(128) +1) =(2^8 −1)(2^8 +1)...(2^(128) +1) ... =(2^(128) −1)(2^(128) +1) =2^(256) −1
$$\left(\mathrm{2}^{\mathrm{1}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{4}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{8}} +\mathrm{1}\right)….\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$=\left(\mathrm{2}^{\mathrm{4}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{4}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{8}} +\mathrm{1}\right)…\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$=\left(\mathrm{2}^{\mathrm{8}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{8}} +\mathrm{1}\right)…\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$… \\ $$$$=\left(\mathrm{2}^{\mathrm{128}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$=\mathrm{2}^{\mathrm{256}} −\mathrm{1} \\ $$
Commented by FilupS last updated on 19/Feb/17
I don′t understand this can you please explain?
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{this} \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{explain}? \\ $$
Commented by mrW1 last updated on 19/Feb/17
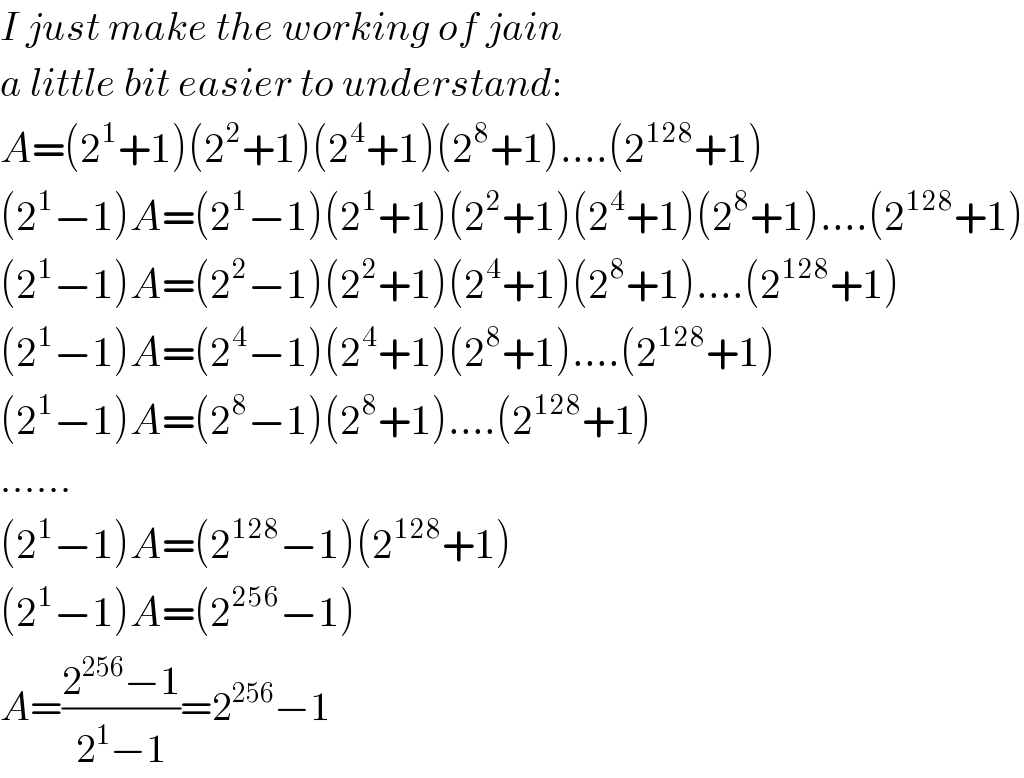
I just make the working of jain a little bit easier to understand: A=(2^1 +1)(2^2 +1)(2^4 +1)(2^8 +1)....(2^(128) +1) (2^1 −1)A=(2^1 −1)(2^1 +1)(2^2 +1)(2^4 +1)(2^8 +1)....(2^(128) +1) (2^1 −1)A=(2^2 −1)(2^2 +1)(2^4 +1)(2^8 +1)....(2^(128) +1) (2^1 −1)A=(2^4 −1)(2^4 +1)(2^8 +1)....(2^(128) +1) (2^1 −1)A=(2^8 −1)(2^8 +1)....(2^(128) +1) ...... (2^1 −1)A=(2^(128) −1)(2^(128) +1) (2^1 −1)A=(2^(256) −1) A=((2^(256) −1)/(2^1 −1))=2^(256) −1
$${I}\:{just}\:{make}\:{the}\:{working}\:{of}\:{jain} \\ $$$${a}\:{little}\:{bit}\:{easier}\:{to}\:{understand}: \\ $$$${A}=\left(\mathrm{2}^{\mathrm{1}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{4}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{8}} +\mathrm{1}\right)….\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$\left(\mathrm{2}^{\mathrm{1}} −\mathrm{1}\right){A}=\left(\mathrm{2}^{\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{1}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{4}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{8}} +\mathrm{1}\right)….\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$\left(\mathrm{2}^{\mathrm{1}} −\mathrm{1}\right){A}=\left(\mathrm{2}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{4}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{8}} +\mathrm{1}\right)….\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$\left(\mathrm{2}^{\mathrm{1}} −\mathrm{1}\right){A}=\left(\mathrm{2}^{\mathrm{4}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{4}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{8}} +\mathrm{1}\right)….\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$\left(\mathrm{2}^{\mathrm{1}} −\mathrm{1}\right){A}=\left(\mathrm{2}^{\mathrm{8}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{8}} +\mathrm{1}\right)….\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$…… \\ $$$$\left(\mathrm{2}^{\mathrm{1}} −\mathrm{1}\right){A}=\left(\mathrm{2}^{\mathrm{128}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{128}} +\mathrm{1}\right) \\ $$$$\left(\mathrm{2}^{\mathrm{1}} −\mathrm{1}\right){A}=\left(\mathrm{2}^{\mathrm{256}} −\mathrm{1}\right) \\ $$$${A}=\frac{\mathrm{2}^{\mathrm{256}} −\mathrm{1}}{\mathrm{2}^{\mathrm{1}} −\mathrm{1}}=\mathrm{2}^{\mathrm{256}} −\mathrm{1} \\ $$
Commented by mrW1 last updated on 19/Feb/17
see also Q#10005
$${see}\:{also}\:{Q}#\mathrm{10005} \\ $$
Commented by sandy_suhendra last updated on 19/Feb/17
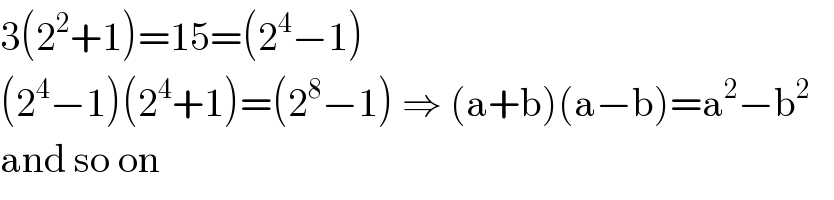
3(2^2 +1)=15=(2^4 −1) (2^4 −1)(2^4 +1)=(2^8 −1) ⇒ (a+b)(a−b)=a^2 −b^2 and so on
$$\mathrm{3}\left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{15}=\left(\mathrm{2}^{\mathrm{4}} −\mathrm{1}\right) \\ $$$$\left(\mathrm{2}^{\mathrm{4}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{4}} +\mathrm{1}\right)=\left(\mathrm{2}^{\mathrm{8}} −\mathrm{1}\right)\:\Rightarrow\:\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}−\mathrm{b}\right)=\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \:\:\: \\ $$$$\mathrm{and}\:\mathrm{so}\:\mathrm{on} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *