Question Number 628 by malwaan last updated on 14/Feb/15
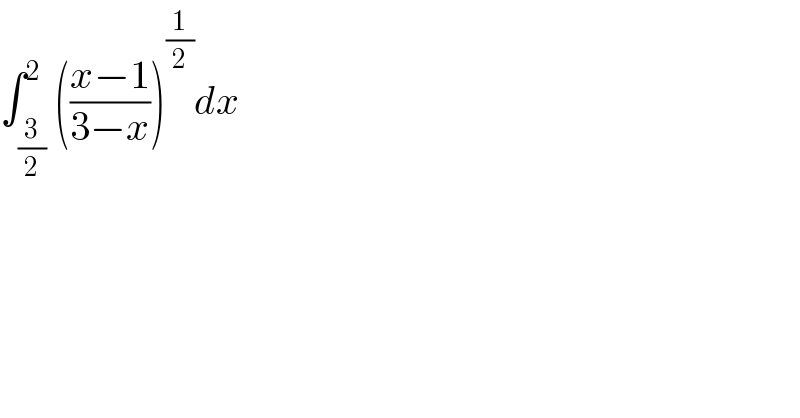
$$\int_{\frac{\mathrm{3}}{\mathrm{2}}} ^{\mathrm{2}} \left(\frac{{x}−\mathrm{1}}{\mathrm{3}−{x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$
Commented by malwaan1 last updated on 26/Feb/15
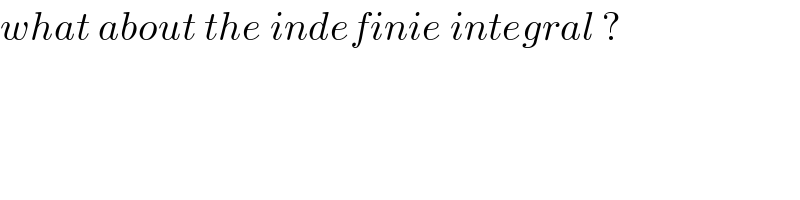
$${what}\:{about}\:{the}\:{indefinie}\:{integral}\:? \\ $$
Answered by prakash jain last updated on 14/Feb/15
![x=t^2 +1 dx=2tdt ((x−1)/(3−x)) =(t^2 /(3−(1+t^2 )))=(t^2 /(2−t^2 )) ∫(√((x−1)/(3−x)))=∫((2t^2 dt)/( (√(2−t^2 )))) =∫((2t^2 −4)/( (√(2−t^2 )))) dt+∫(4/( (√(2−t^2 ))))dt =−2∫(√(2−t^2 ))dt+∫(4/( (√(2−t^2 ))))dt =−2[(1/2)t(√(2−t^2 ))+sin^(−1) (t/( (√2)))]+4sin^(−1) (t/( (√2))) =2sin^(−1) (t/( (√2)))−t(√(2−t^2 )) =2sin^(−1) (√((x−1)/2))−(√(x−1))(√(3−x)) [2sin^(−1) (√((x−1)/2))−(√(x−1))(√(3−x))]_(3/2) ^2 =[2sin^(−1) (√(1/2))−1]−[2sin^(−1) (√(1/4))−(√(1/2))(√(3/2))] =2(π/4)−1−2(π/6)+((√3)/2) =(π/2) − (π/3)+(((√3) −2)/2) =(π/6) +(((√3) −2)/2)](https://www.tinkutara.com/question/Q629.png)
$${x}={t}^{\mathrm{2}} +\mathrm{1} \\ $$$${dx}=\mathrm{2}{tdt} \\ $$$$\frac{{x}−\mathrm{1}}{\mathrm{3}−{x}}\:=\frac{{t}^{\mathrm{2}} }{\mathrm{3}−\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}=\frac{{t}^{\mathrm{2}} }{\mathrm{2}−{t}^{\mathrm{2}} } \\ $$$$\int\sqrt{\frac{{x}−\mathrm{1}}{\mathrm{3}−{x}}}=\int\frac{\mathrm{2}{t}^{\mathrm{2}} \:{dt}}{\:\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }} \\ $$$$=\int\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{4}}{\:\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }}\:{dt}+\int\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }}{dt} \\ $$$$=−\mathrm{2}\int\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }{dt}+\int\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }}{dt} \\ $$$$=−\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{2}}{t}\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }+\mathrm{sin}^{−\mathrm{1}} \frac{{t}}{\:\sqrt{\mathrm{2}}}\right]+\mathrm{4sin}^{−\mathrm{1}} \frac{{t}}{\:\sqrt{\mathrm{2}}} \\ $$$$=\mathrm{2sin}^{−\mathrm{1}} \frac{{t}}{\:\sqrt{\mathrm{2}}}−{t}\sqrt{\mathrm{2}−{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2sin}^{−\mathrm{1}} \sqrt{\frac{{x}−\mathrm{1}}{\mathrm{2}}}−\sqrt{{x}−\mathrm{1}}\sqrt{\mathrm{3}−{x}} \\ $$$$\left[\mathrm{2sin}^{−\mathrm{1}} \sqrt{\frac{{x}−\mathrm{1}}{\mathrm{2}}}−\sqrt{{x}−\mathrm{1}}\sqrt{\mathrm{3}−{x}}\right]_{\mathrm{3}/\mathrm{2}} ^{\mathrm{2}} \\ $$$$=\left[\mathrm{2sin}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}}{\mathrm{2}}}−\mathrm{1}\right]−\left[\mathrm{2sin}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}}{\mathrm{4}}}−\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right] \\ $$$$=\mathrm{2}\frac{\pi}{\mathrm{4}}−\mathrm{1}−\mathrm{2}\frac{\pi}{\mathrm{6}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\:\frac{\pi}{\mathrm{3}}+\frac{\sqrt{\mathrm{3}}\:−\mathrm{2}}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{6}}\:+\frac{\sqrt{\mathrm{3}}\:−\mathrm{2}}{\mathrm{2}} \\ $$
Commented by malwaan last updated on 03/Mar/15

$${please}\:{solve}\:{the}\:{integral}\:{by}\:{sub}.\:{x}=\mathrm{2}−{cos}\:\theta \\ $$$${whay}\:{the}\:{result}\:{is}\:{different}\:? \\ $$
Commented by prakash jain last updated on 03/Mar/15

$$\mathrm{I}\:\mathrm{reposted}\:\mathrm{a}\:\mathrm{question}\:−\:\mathrm{may} \\ $$$$\mathrm{be}\:\mathrm{you}\:\mathrm{can}\:\mathrm{write}\:\mathrm{what}\:\mathrm{you}\:\mathrm{got}\:\mathrm{in}\:\mathrm{that}\:\mathrm{approach}. \\ $$
Commented by malwaan last updated on 03/Mar/15

$${I}\:{am}\:{sorry}\: \\ $$$${x}=\mathrm{2}−{cos}\theta \\ $$
