Question Number 711 by prakash jain last updated on 03/Mar/15
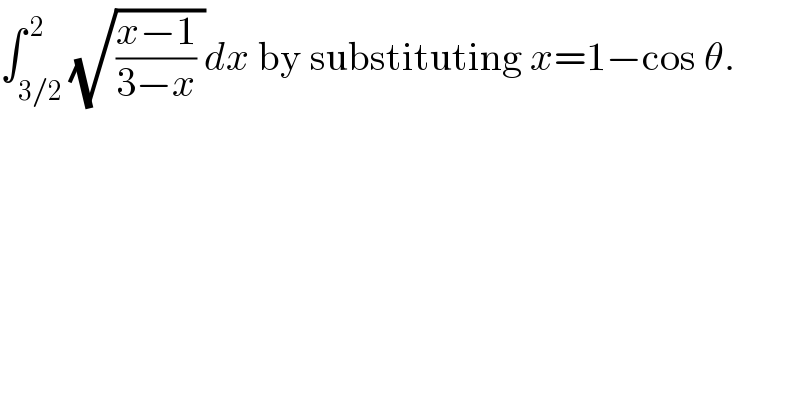
$$\int_{\mathrm{3}/\mathrm{2}} ^{\:\mathrm{2}} \sqrt{\frac{{x}−\mathrm{1}}{\mathrm{3}−{x}}\:}{dx}\:\mathrm{by}\:\mathrm{substituting}\:{x}=\mathrm{1}−\mathrm{cos}\:\theta. \\ $$
Commented by malwaan last updated on 03/Mar/15

$${I}\:{am}\:{sorry} \\ $$$${x}=\mathrm{2}−{cos}\theta \\ $$
Answered by prakash jain last updated on 03/Mar/15
![x=2−cos θ dx=sin θ dθ=2sin (θ/2)cos (θ/2) x=3/2⇒θ=π/3, x=2⇒θ=π (√((x−1)/(3+x)))=(√((1−cos θ)/(1+cos θ)))=tan (θ/2) ∫_(π/3) ^( π/2) 2sin (θ/2)cos (θ/2)tan (θ/2) dθ ∫_(π/3) ^( π/2) 2sin^2 (θ/2) dθ ∫_(π/3) ^( π/2) (1−cos θ) dθ =[θ−sin θ]_(π/3) ^(π/2) =((π/2)−1)−((π/3)−((√3)/2)) =(π/6)+(((√3)−2)/2) You get the same answer as in the earlier question.](https://www.tinkutara.com/question/Q720.png)
$${x}=\mathrm{2}−\mathrm{cos}\:\theta \\ $$$${dx}=\mathrm{sin}\:\theta\:{d}\theta=\mathrm{2sin}\:\frac{\theta}{\mathrm{2}}\mathrm{cos}\:\frac{\theta}{\mathrm{2}} \\ $$$${x}=\mathrm{3}/\mathrm{2}\Rightarrow\theta=\pi/\mathrm{3},\:{x}=\mathrm{2}\Rightarrow\theta=\pi \\ $$$$\sqrt{\frac{{x}−\mathrm{1}}{\mathrm{3}+{x}}}=\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta}}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\int_{\pi/\mathrm{3}} ^{\:\pi/\mathrm{2}} \mathrm{2sin}\:\frac{\theta}{\mathrm{2}}\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:{d}\theta \\ $$$$\int_{\pi/\mathrm{3}} ^{\:\pi/\mathrm{2}} \mathrm{2sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\:{d}\theta \\ $$$$\int_{\pi/\mathrm{3}} ^{\:\pi/\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)\:{d}\theta \\ $$$$=\left[\theta−\mathrm{sin}\:\theta\right]_{\pi/\mathrm{3}} ^{\pi/\mathrm{2}} \\ $$$$=\left(\frac{\pi}{\mathrm{2}}−\mathrm{1}\right)−\left(\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$=\frac{\pi}{\mathrm{6}}+\frac{\sqrt{\mathrm{3}}−\mathrm{2}}{\mathrm{2}} \\ $$$$\mathrm{You}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{answer}\:\mathrm{as}\:\mathrm{in}\:\mathrm{the}\:\mathrm{earlier} \\ $$$$\mathrm{question}. \\ $$
Commented by malwaan1 last updated on 04/Mar/15

$${thank}\:{you} \\ $$
Commented by malwaan last updated on 04/Mar/15
$${I}\:{will}\:{send}\:{my}\:{answer}\:{soon} \\ $$
