Menu Close

3-2-log-9-25-5-9-2-x-

Tinku Tara 0 Comments
Pin




Question Number 4515 by love math last updated on 04/Feb/16
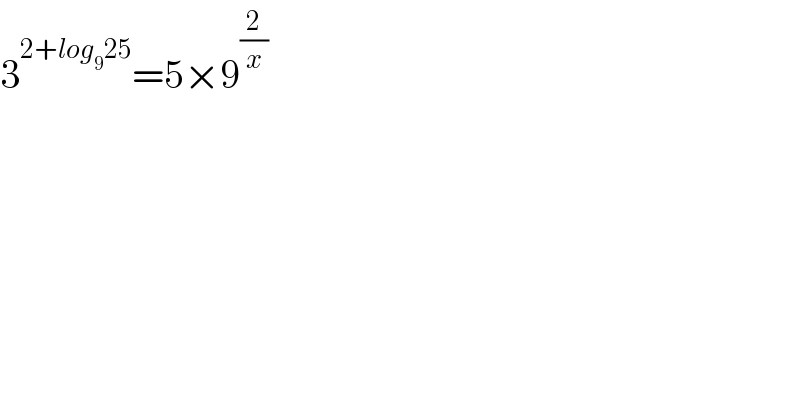
3^(2+log_9 25) =5×9^(2/x)
$$\mathrm{3}^{\mathrm{2}+{log}_{\mathrm{9}} \mathrm{25}} =\mathrm{5}×\mathrm{9}^{\frac{\mathrm{2}}{{x}}} \\ $$
Commented by love math last updated on 05/Feb/16
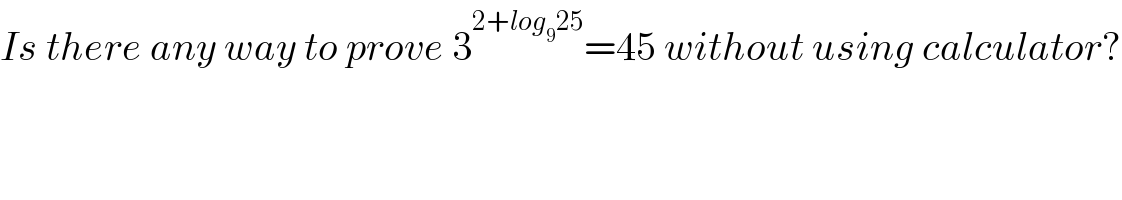
Is there any way to prove 3^(2+log_9 25) =45 without using calculator?
$${Is}\:{there}\:{any}\:{way}\:{to}\:{prove}\:\mathrm{3}^{\mathrm{2}+{log}_{\mathrm{9}} \mathrm{25}} =\mathrm{45}\:{without}\:{using}\:{calculator}? \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 06/Feb/16
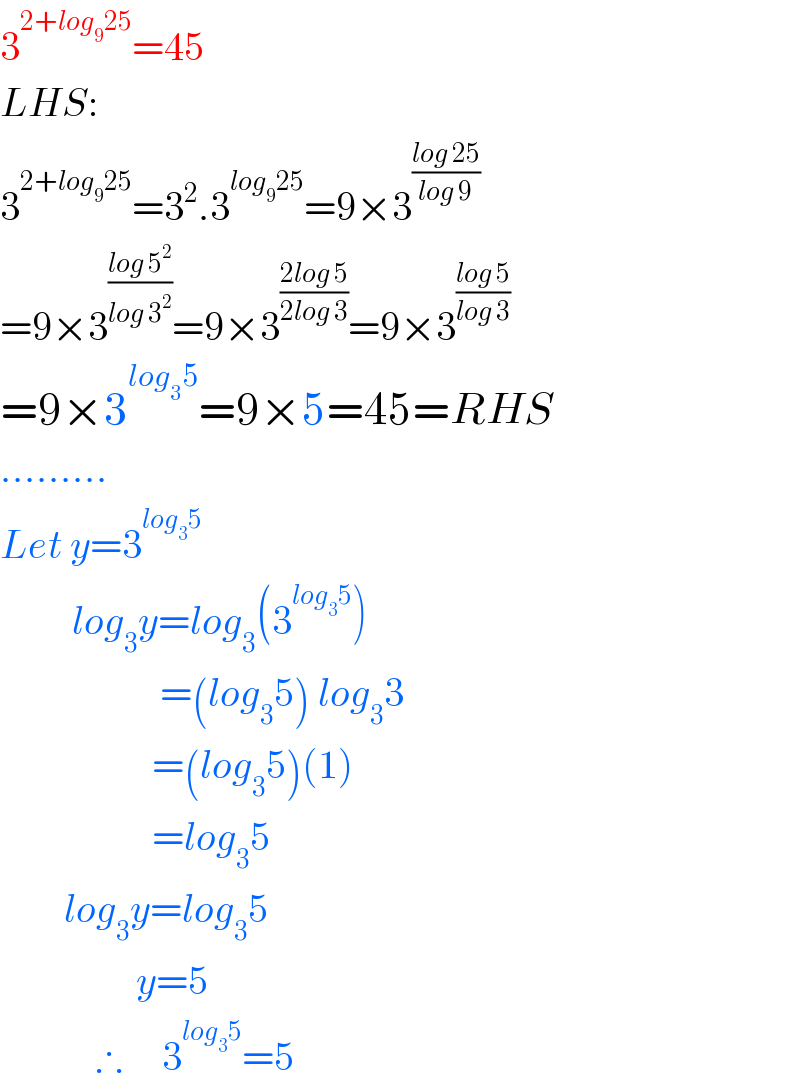
3^(2+log_9 25) =45 LHS: 3^(2+log_9 25) =3^2 .3^(log_9 25) =9×3^((log 25)/(log 9)) =9×3^((log 5^2 )/(log 3^2 )) =9×3^((2log 5)/(2log 3)) =9×3^((log 5)/(log 3)) =9×3^(log_3 5) =9×5=45=RHS ......... Let y=3^(log_3 5) log_3 y=log_3 (3^(log_3 5) ) =(log_3 5) log_3 3 =(log_3 5)(1) =log_3 5 log_3 y=log_3 5 y=5 ∴ 3^(log_3 5) =5
$$\mathrm{3}^{\mathrm{2}+{log}_{\mathrm{9}} \mathrm{25}} =\mathrm{45} \\ $$$${LHS}: \\ $$$$\mathrm{3}^{\mathrm{2}+{log}_{\mathrm{9}} \mathrm{25}} =\mathrm{3}^{\mathrm{2}} .\mathrm{3}^{{log}_{\mathrm{9}} \mathrm{25}} =\mathrm{9}×\mathrm{3}^{\frac{{log}\:\mathrm{25}}{{log}\:\mathrm{9}}} \\ $$$$=\mathrm{9}×\mathrm{3}^{\frac{{log}\:\mathrm{5}^{\mathrm{2}} }{{log}\:\mathrm{3}^{\mathrm{2}} }} =\mathrm{9}×\mathrm{3}^{\frac{\mathrm{2}{log}\:\mathrm{5}}{\mathrm{2}{log}\:\mathrm{3}}} =\mathrm{9}×\mathrm{3}^{\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}}} \\ $$$$=\mathrm{9}×\mathrm{3}^{{log}_{\mathrm{3}} \mathrm{5}} =\mathrm{9}×\mathrm{5}=\mathrm{45}={RHS} \\ $$$$……… \\ $$$${Let}\:{y}=\mathrm{3}^{{log}_{\mathrm{3}} \mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:{log}_{\mathrm{3}} {y}={log}_{\mathrm{3}} \left(\mathrm{3}^{{log}_{\mathrm{3}} \mathrm{5}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({log}_{\mathrm{3}} \mathrm{5}\right)\:{log}_{\mathrm{3}} \mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({log}_{\mathrm{3}} \mathrm{5}\right)\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={log}_{\mathrm{3}} \mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:{log}_{\mathrm{3}} {y}={log}_{\mathrm{3}} \mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\:\:\:\:\mathrm{3}^{{log}_{\mathrm{3}} \mathrm{5}} =\mathrm{5} \\ $$
Answered by Rasheed Soomro last updated on 05/Feb/16
3^(2+log_9 25) =5×9^(2/x) In order to write 5 as power of 3 : let 3^y =5 ylog 3=log 5 y=((log 5)/(log 3)) 3^(2+log_9 25) =3^((log 5)/(log 3)) ×3^(4/x) 3^(2+log_9 25) =3^(((log 5)/(log 3))+(4/x)) ((log 5)/(log 3))+(4/x)=2+log_9 25 ((log 5)/(log 3))+(4/x)=2+((log 25)/(log 9)) ((log 5)/(log 3))+(4/x)=2+((log 5^2 )/(log 3^2 )) ((log 5)/(log 3))+(4/x)=2+((2log 5)/(2log 3)) ((log 5)/(log 3))+(4/x)=2+((log 5)/(log 3)) (4/x)=2 x=2
$$\mathrm{3}^{\mathrm{2}+{log}_{\mathrm{9}} \mathrm{25}} =\mathrm{5}×\mathrm{9}^{\frac{\mathrm{2}}{{x}}} \\ $$$${In}\:{order}\:{to}\:{write}\:\mathrm{5}\:{as}\:{power}\:{of}\:\mathrm{3}\::\: \\ $$$${let}\:\mathrm{3}^{{y}} =\mathrm{5} \\ $$$$\:\:\:\:\:{ylog}\:\mathrm{3}={log}\:\mathrm{5} \\ $$$$\:\:\:\:\:{y}=\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}} \\ $$$$\mathrm{3}^{\mathrm{2}+{log}_{\mathrm{9}} \mathrm{25}} =\mathrm{3}^{\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}}} ×\mathrm{3}^{\frac{\mathrm{4}}{{x}}} \\ $$$$\mathrm{3}^{\mathrm{2}+{log}_{\mathrm{9}} \mathrm{25}} =\mathrm{3}^{\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}}+\frac{\mathrm{4}}{{x}}} \\ $$$$\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}}+\frac{\mathrm{4}}{{x}}=\mathrm{2}+{log}_{\mathrm{9}} \mathrm{25} \\ $$$$\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}}+\frac{\mathrm{4}}{{x}}=\mathrm{2}+\frac{{log}\:\mathrm{25}}{{log}\:\mathrm{9}} \\ $$$$\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}}+\frac{\mathrm{4}}{{x}}=\mathrm{2}+\frac{{log}\:\mathrm{5}^{\mathrm{2}} }{{log}\:\mathrm{3}^{\mathrm{2}} } \\ $$$$\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}}+\frac{\mathrm{4}}{{x}}=\mathrm{2}+\frac{\mathrm{2}{log}\:\mathrm{5}}{\mathrm{2}{log}\:\mathrm{3}} \\ $$$$\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}}+\frac{\mathrm{4}}{{x}}=\mathrm{2}+\frac{{log}\:\mathrm{5}}{{log}\:\mathrm{3}} \\ $$$$\frac{\mathrm{4}}{{x}}=\mathrm{2} \\ $$$${x}=\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *