Question Number 10206 by konen last updated on 30/Jan/17
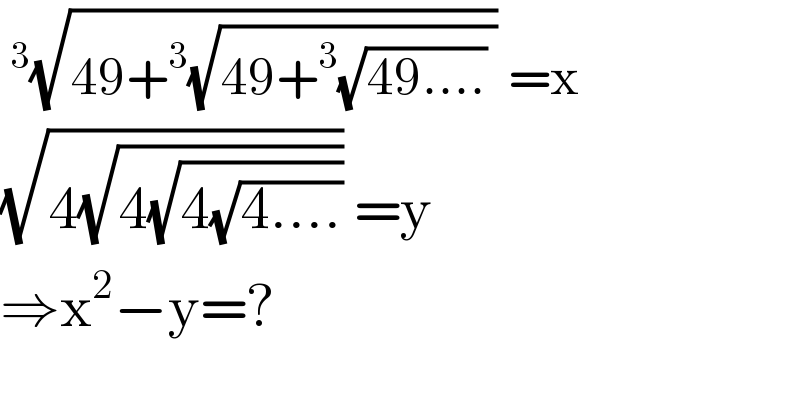
$$\:^{\mathrm{3}} \sqrt{\mathrm{49}+^{\mathrm{3}} \sqrt{\mathrm{49}+^{\mathrm{3}} \sqrt{\mathrm{49}….}\:}}\:=\mathrm{x} \\ $$$$\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}….}}}}\:=\mathrm{y} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{y}=? \\ $$
Answered by FilupSmith last updated on 30/Jan/17
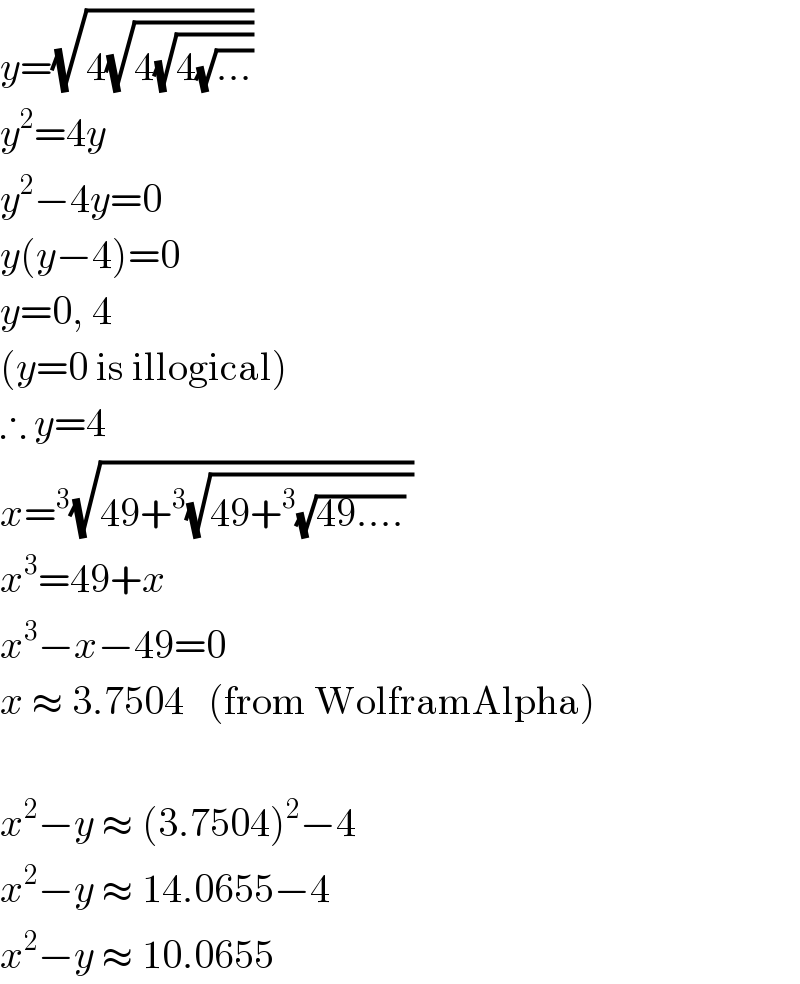
$${y}=\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{…}}}} \\ $$$${y}^{\mathrm{2}} =\mathrm{4}{y} \\ $$$${y}^{\mathrm{2}} −\mathrm{4}{y}=\mathrm{0} \\ $$$${y}\left({y}−\mathrm{4}\right)=\mathrm{0} \\ $$$${y}=\mathrm{0},\:\mathrm{4} \\ $$$$\left({y}=\mathrm{0}\:\mathrm{is}\:\mathrm{illogical}\right) \\ $$$$\therefore\:{y}=\mathrm{4} \\ $$$${x}=^{\mathrm{3}} \sqrt{\mathrm{49}+^{\mathrm{3}} \sqrt{\mathrm{49}+^{\mathrm{3}} \sqrt{\mathrm{49}….}\:}} \\ $$$${x}^{\mathrm{3}} =\mathrm{49}+{x} \\ $$$${x}^{\mathrm{3}} −{x}−\mathrm{49}=\mathrm{0} \\ $$$${x}\:\approx\:\mathrm{3}.\mathrm{7504}\:\:\:\left(\mathrm{from}\:\mathrm{WolframAlpha}\right) \\ $$$$\: \\ $$$${x}^{\mathrm{2}} −{y}\:\approx\:\left(\mathrm{3}.\mathrm{7504}\right)^{\mathrm{2}} −\mathrm{4} \\ $$$${x}^{\mathrm{2}} −{y}\:\approx\:\mathrm{14}.\mathrm{0655}−\mathrm{4} \\ $$$${x}^{\mathrm{2}} −{y}\:\approx\:\mathrm{10}.\mathrm{0655} \\ $$
