Question Number 10197 by konen last updated on 29/Jan/17
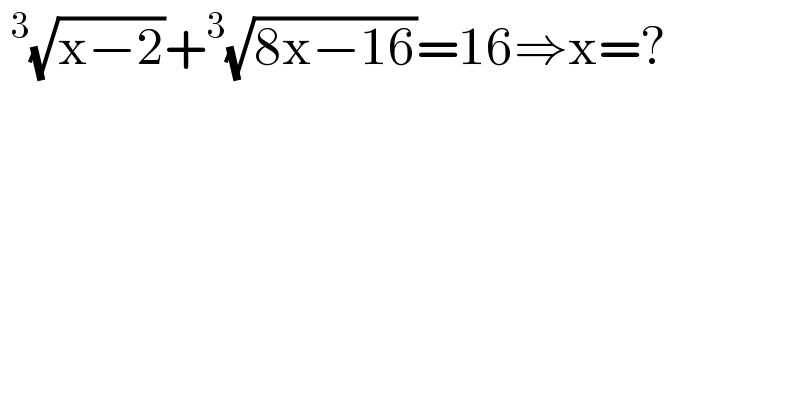
$$\:^{\mathrm{3}} \sqrt{\mathrm{x}−\mathrm{2}}+^{\mathrm{3}} \sqrt{\mathrm{8x}−\mathrm{16}}=\mathrm{16}\Rightarrow\mathrm{x}=? \\ $$
Answered by sandy_suhendra last updated on 29/Jan/17
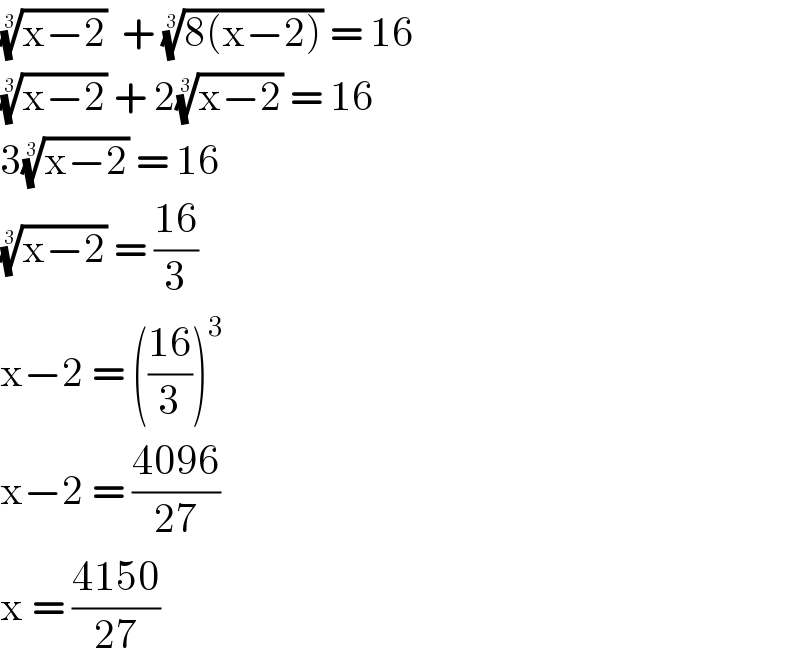
$$\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{2}}\:\:+\:\sqrt[{\mathrm{3}}]{\mathrm{8}\left(\mathrm{x}−\mathrm{2}\right)}\:=\:\mathrm{16} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{2}}\:+\:\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{2}}\:=\:\mathrm{16} \\ $$$$\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{2}}\:=\:\mathrm{16} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{2}}\:=\:\frac{\mathrm{16}}{\mathrm{3}} \\ $$$$\mathrm{x}−\mathrm{2}\:=\:\left(\frac{\mathrm{16}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$\mathrm{x}−\mathrm{2}\:=\:\frac{\mathrm{4096}}{\mathrm{27}} \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{4150}}{\mathrm{27}} \\ $$
