Question Number 13002 by Joel577 last updated on 10/May/17
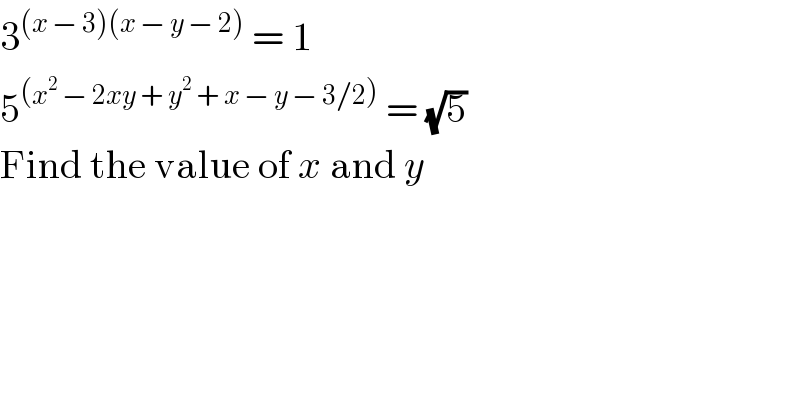
$$\mathrm{3}^{\left({x}\:−\:\mathrm{3}\right)\left({x}\:−\:{y}\:−\:\mathrm{2}\right)} \:=\:\mathrm{1} \\ $$$$\mathrm{5}^{\left({x}^{\mathrm{2}} \:−\:\mathrm{2}{xy}\:+\:{y}^{\mathrm{2}} \:+\:{x}\:−\:{y}\:−\:\mathrm{3}/\mathrm{2}\right)} \:=\:\sqrt{\mathrm{5}} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x}\:\mathrm{and}\:{y} \\ $$
Answered by 433 last updated on 10/May/17
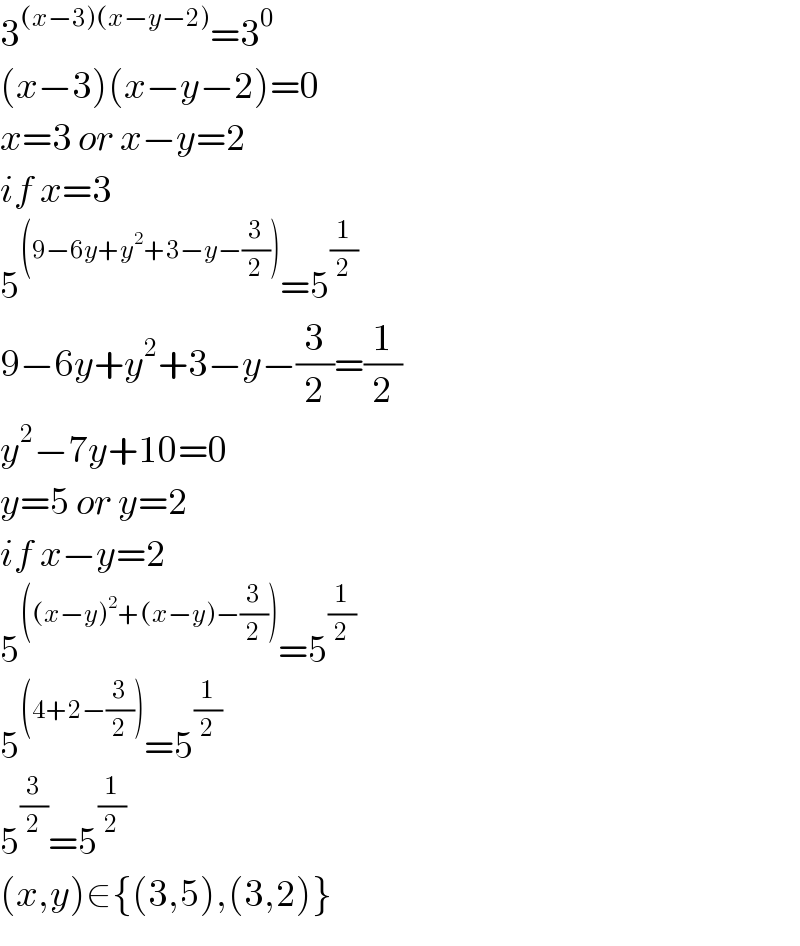
$$\mathrm{3}^{\left({x}−\mathrm{3}\right)\left({x}−{y}−\mathrm{2}\right)} =\mathrm{3}^{\mathrm{0}} \\ $$$$\left({x}−\mathrm{3}\right)\left({x}−{y}−\mathrm{2}\right)=\mathrm{0} \\ $$$${x}=\mathrm{3}\:{or}\:{x}−{y}=\mathrm{2} \\ $$$${if}\:{x}=\mathrm{3} \\ $$$$\mathrm{5}^{\left(\mathrm{9}−\mathrm{6}{y}+{y}^{\mathrm{2}} +\mathrm{3}−{y}−\frac{\mathrm{3}}{\mathrm{2}}\right)} =\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{9}−\mathrm{6}{y}+{y}^{\mathrm{2}} +\mathrm{3}−{y}−\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −\mathrm{7}{y}+\mathrm{10}=\mathrm{0} \\ $$$${y}=\mathrm{5}\:{or}\:{y}=\mathrm{2} \\ $$$${if}\:{x}−{y}=\mathrm{2} \\ $$$$\mathrm{5}^{\left(\left({x}−{y}\right)^{\mathrm{2}} +\left({x}−{y}\right)−\frac{\mathrm{3}}{\mathrm{2}}\right)} =\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{5}^{\left(\mathrm{4}+\mathrm{2}−\frac{\mathrm{3}}{\mathrm{2}}\right)} =\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{5}^{\frac{\mathrm{3}}{\mathrm{2}}} =\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{2}}} \: \\ $$$$\left({x},{y}\right)\in\left\{\left(\mathrm{3},\mathrm{5}\right),\left(\mathrm{3},\mathrm{2}\right)\right\} \\ $$
Commented by Joel577 last updated on 11/May/17
$${thank}\:{you}\:{very}\:{much} \\ $$
