Question Number 72190 by oyemi kemewari last updated on 26/Oct/19
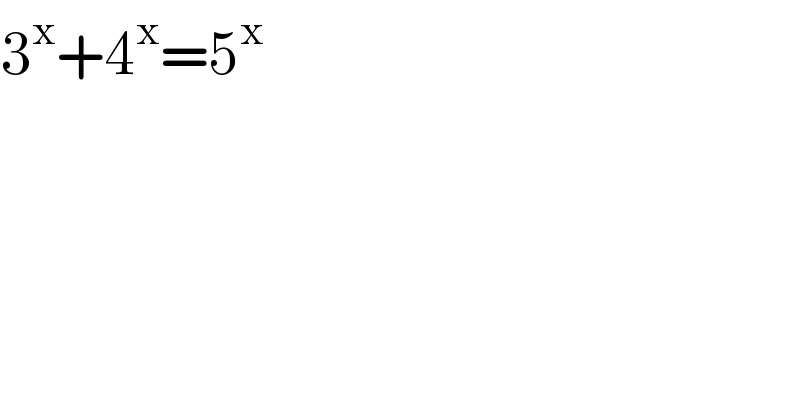
$$\mathrm{3}^{\mathrm{x}} +\mathrm{4}^{\mathrm{x}} =\mathrm{5}^{\mathrm{x}} \\ $$
Commented by oyemi kemewari last updated on 26/Oct/19
find x
Commented by Joel578 last updated on 26/Oct/19

$${x}\:=\:\mathrm{2} \\ $$
Answered by mind is power last updated on 27/Oct/19
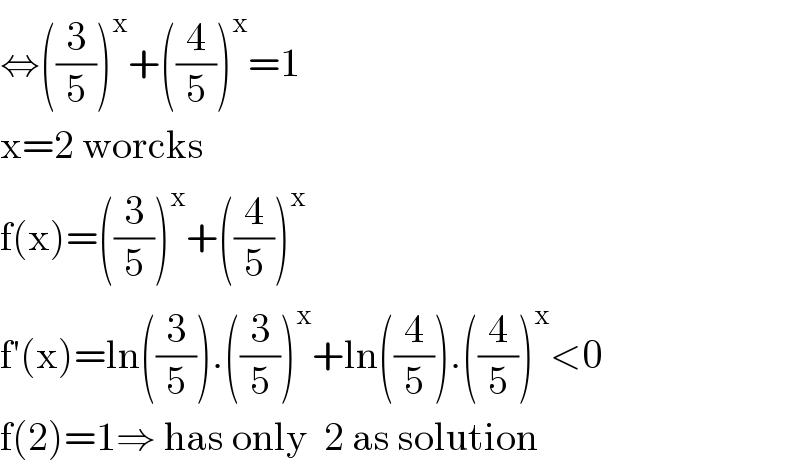
$$\Leftrightarrow\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{x}} +\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{x}} =\mathrm{1} \\ $$$$\mathrm{x}=\mathrm{2}\:\mathrm{worcks} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{x}} +\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{x}} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{5}}\right).\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{x}} +\mathrm{ln}\left(\frac{\mathrm{4}}{\mathrm{5}}\right).\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{x}} <\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{2}\right)=\mathrm{1}\Rightarrow\:\mathrm{has}\:\mathrm{only}\:\:\mathrm{2}\:\mathrm{as}\:\mathrm{solution} \\ $$
Commented by Rasheed.Sindhi last updated on 27/Oct/19
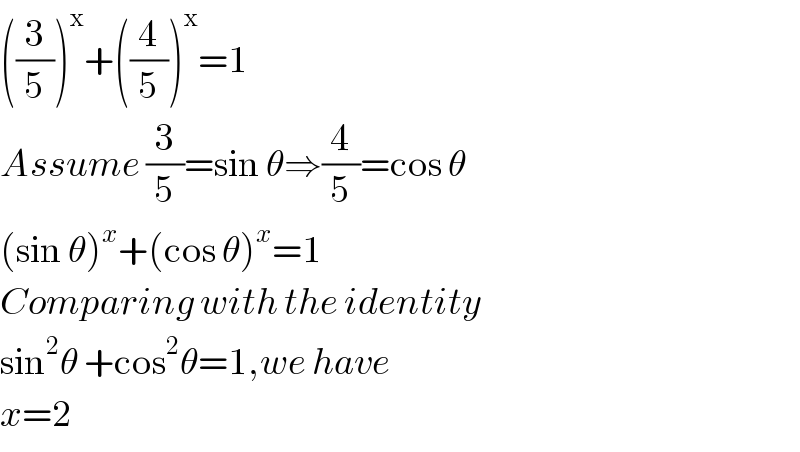
$$\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{x}} +\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{x}} =\mathrm{1} \\ $$$${Assume}\:\frac{\mathrm{3}}{\mathrm{5}}=\mathrm{sin}\:\theta\Rightarrow\frac{\mathrm{4}}{\mathrm{5}}=\mathrm{cos}\:\theta \\ $$$$\left(\mathrm{sin}\:\theta\right)^{{x}} +\left(\mathrm{cos}\:\theta\right)^{{x}} =\mathrm{1} \\ $$$${Comparing}\:{with}\:{the}\:{identity} \\ $$$$\mathrm{sin}^{\mathrm{2}} \theta\:+\mathrm{cos}^{\mathrm{2}} \theta=\mathrm{1},{we}\:{have}\: \\ $$$${x}=\mathrm{2} \\ $$
